淄博手机网站建设千锋教育前端学费多少

题目列表

2873. 有序三元组中的最大值 I

2874. 有序三元组中的最大值 II

2875. 无限数组的最短子数组

2876. 有向图访问计数

 一、有序三元组中的最大值I

 看一眼该题的数据范围，直接三层for循环暴力枚举，时间复杂度O(n^3)，代码如下

class Solution {
public:long long maximumTripletValue(vector<int>& nums) {long long ans=0;for(int i=0;i<nums.size();i++){for(int j=i+1;j<nums.size();j++){for(int k=j+1;k<nums.size();k++){ans=max(ans,1LL*(nums[i]-nums[j])*nums[k]);}}}return ans;}
};

二、有序三元组的最大值II

题目同上一题，只有数据范围不同

同一个题，数据范围变大之后，再用暴力就会超时，我们要想想怎么优化时间复杂度 ？

这里有三种思路：

1.我们枚举i，看j，k怎么选？

2.我们枚举j，看i，k怎么选？

3.我们枚举k，看i，j怎么选？

假设我们选择方案一：枚举i(即先确定一个nums[ i ])，那么nums[ j ]和nums[ k ]要如何选？才能让三元组的值最大，显然nums[ j ]要选最小的，nums[ k ]选最大的，这样三元组值最大，但是还有一个条件j<k，这就很难办了， 因为我们不能确定要选择的最小值和最大值的位置关系，所以方案一不选

假设我们选择方案二：枚举j(即先确定一个nums[ j ])，那么nums[ i ]和nums[ k ]要如何选？才能让三元组的值最大，显然nums[ i ]选最大的，nums[ k ]也选最大的，这样三元组值最大，并且i<j<k，即我们选取的nums[ i ]和nums[ k ]是互不影响的，我们只要预处理出前i个元素的最大值，和后i个元素的最大值，就能在O(n)的时间复杂度内找到答案，代码如下

class Solution {
public:long long maximumTripletValue(vector<int>& nums) {int n=nums.size();long long ans=0;vector<int>pre(n+1),suf(n);pre[0]=0;for(int i=0;i<n;i++)pre[i+1]=max(pre[i],nums[i]);for(int i=n-1;i>=1;i--)suf[i-1]=max(suf[i],nums[i]);for(int j=0;j<n;j++)ans=max(ans,1LL*(pre[j]-nums[j])*suf[j]);return ans;}
};//当然这里的前缀最大值数组还可以优化掉
class Solution {
public:long long maximumTripletValue(vector<int>& nums) {int n=nums.size();long long ans=0;vector<int>suf(n);for(int i=n-1;i>=1;i--)suf[i-1]=max(suf[i],nums[i]);for(int j=1,pre=nums[0];j<n;j++){ans=max(ans,1LL*(pre-nums[j])*suf[j]);pre=max(pre,nums[j]);}return ans;}
};

假设我们选择方案三：枚举k(即先确定一个nums[ k ])，那么nums[ i ]和nums[ j ]要如何选？才能让三元组的值最大，即nums[ i ] - nums[ j ]要最大，那么这不就是在遍历的过程中，维护一个前缀最大值和一个最大高度差吗，(估计有人不太能理解，我画个折线图，大家应该能好懂一些，思路和121. 买卖股票的最佳时机很相似）

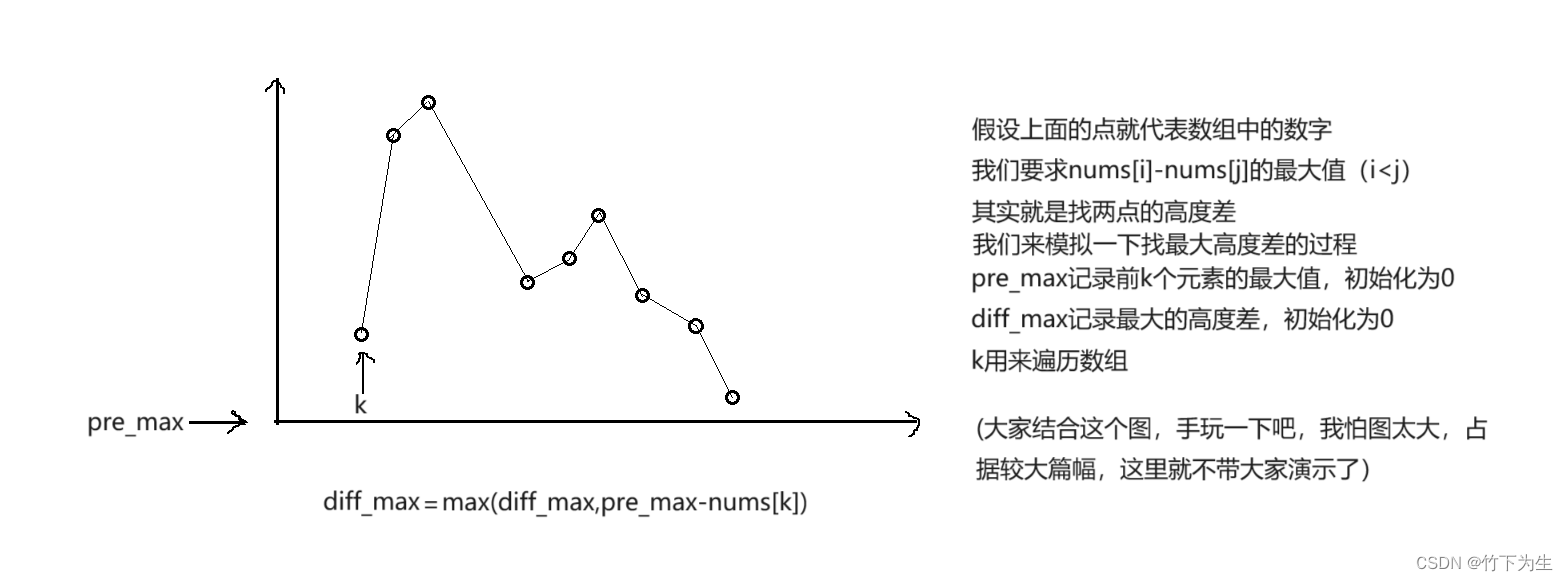
代码如下

class Solution {
public:long long maximumTripletValue(vector<int>& nums) {int n=nums.size();long long ans=0;for(int k=0,pre=0,diff=0;k<n;k++){ans=max(ans,1LL*diff*nums[k]);diff=max(diff,pre-nums[k]);pre=max(pre,nums[k]);}return ans;}
};

(大家可以试着将第二题的代码放到第一题去跑一跑，对比一下两者的时间，感受一下算法的魅力) 

三、无限数组的最短子数组

看到找最短的子数组的和等于target，第一个想到的就是滑动窗口，当然这题和正常的滑窗有点不同，它给的数组是个可以循环的无限长数组。

我们要弄明白两个问题：

1.我们需要一直遍历到无限远吗？不需要，我们的left端点只要在2倍的该数组里面遍历就行，因为一旦超过这个范围，后面的就又会开始循环之前遍历的结果，没有任何意义。

2.如果target>=sum(nums) ，我们的子数组还需要从0开始增加长度吗？不用，因为不论怎么枚举，子数组的长度都会有length(nums)*(target/sum(nums))的基础长度，我们只要关心target%sum(nums)这部分的最小子数组的长度就可以了，这样我们就将子数组差分成了两个部分，一个是以整个数组为单位的，一个是单独考虑的。

当然肯定有人会怀疑我们这种想法是不是太想当然了，万一这两部分不能形成一个子数组怎么办？好，这里我们就构造一个这样的子数组，我们假定找到了单独考虑的那部分子数组，然后我们继续向后延伸，由于数组是循环的，所以我们总能找到和原数组长度一样的，值相等的区间，如此循环就能构造出我们想要的最短子数组，即上面的想法正确

代码如下

class Solution {
public:typedef long long LL;int minSizeSubarray(vector<int>& nums, int target) {LL sum=accumulate(nums.begin(),nums.end(),0LL);int n=nums.size();int s=0,ans=INT_MAX;for(int left=0,right=0;right<2*n;right++){s+=nums[right%n];while(s>(target%sum)){s-=nums[left%n];left++;}if(s==(target%sum)) ans=min(ans,right-left+1);}if(ans==INT_MAX)return -1;return ans+target/sum*n;}
};

四、有向图访问计数

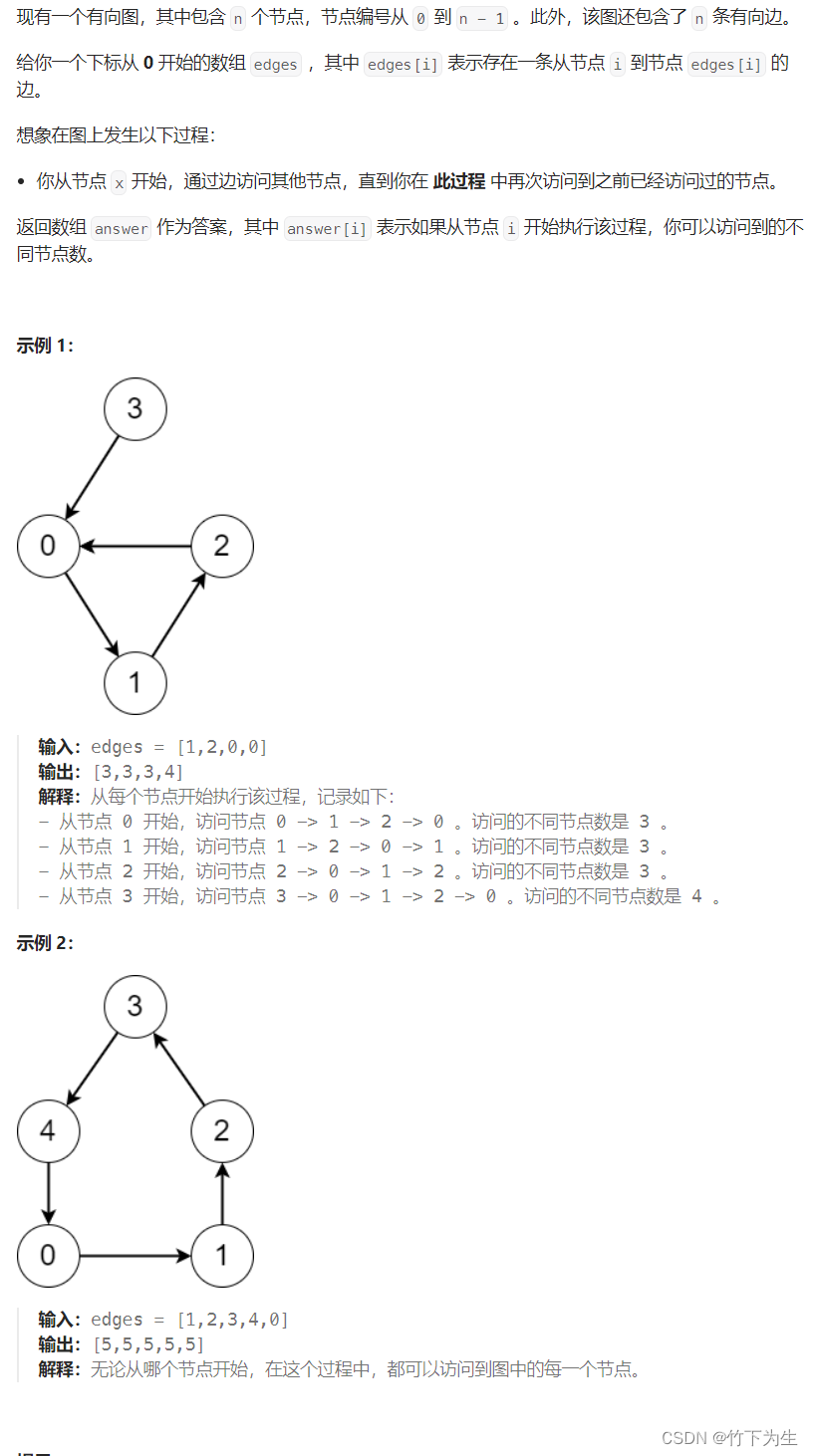
这是一个求每个结点向下能访问多少个不同结点的问题，我们需要用拓扑排序将每个环从图中拆下来单独考虑，得到换上每个结点的访问个数，然后利用返图，计算不在环上的点的访问个数，

代码如下

class Solution {
public:vector<int> countVisitedNodes(vector<int>& edges) {int n=edges.size();vector<vector<int>>g(n);//反图vector<int>deg(n);//入度for(int i=0;i<n;i++){g[edges[i]].push_back(i);deg[edges[i]]++;}//拓扑排序queue<int>q;//存放入读为0的点for(int i=0;i<n;i++){if(deg[i]==0)q.push(i);}//将不在环上的结点从图中去掉，指的是将结点的入度设置为0while(!q.empty()){int x=q.front();q.pop();if(--deg[edges[x]]==0)q.push(edges[x]);}vector<int>ans(n);//计算不在环上的点function<void(int,int)>dfs=[&](int x,int depth){ans[x]=depth;for(int y:g[x]){if(deg[y]==0){//环上的点入度为-1，这里只遍历不在环上的点dfs(y,depth+1);}}};for(int i=0;i<n;i++){if(deg[i]<=0) continue;//先计算环上的点的个数vector<int>node;for(int x=i;;x=edges[x]){node.push_back(x);deg[x]=-1;//被计算过的环上的点的入度设为-1if(edges[x]==i)break;}for(int x:node){dfs(x,node.size());}}return ans;}
};