windows虚拟主机seo的最终是为了达到
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 前言
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:路径总和 II
出处:113. 路径总和 II
难度
4 级
题目描述
要求
给你二叉树的根结点 root \texttt{root} root 和一个表示目标和的整数 targetSum \texttt{targetSum} targetSum,返回所有的满足路径上结点值总和等于目标和 targetSum \texttt{targetSum} targetSum 的从根结点到叶结点的路径。每条路径应该以结点值列表的形式返回,而不是结点的引用。
示例
示例 1:
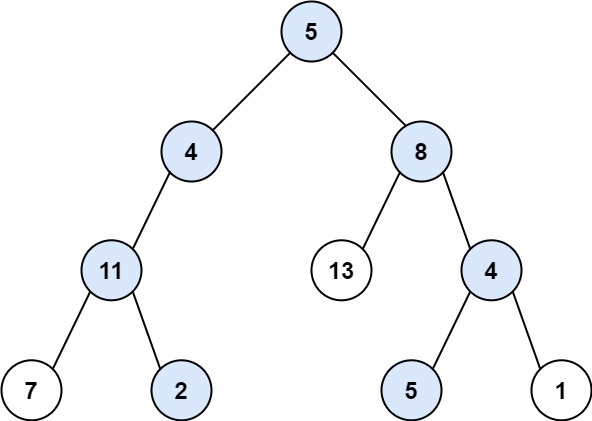
输入: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 \texttt{root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22} root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出: [[5,4,11,2],[5,8,4,5]] \texttt{[[5,4,11,2],[5,8,4,5]]} [[5,4,11,2],[5,8,4,5]]
解释:有两条路径的结点值总和等于 targetSum \texttt{targetSum} targetSum:
5 + 4 + 11 + 2 = 22 \texttt{5 + 4 + 11 + 2 = 22} 5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22 \texttt{5 + 8 + 4 + 5 = 22} 5 + 8 + 4 + 5 = 22
示例 2:
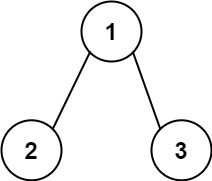
输入: root = [1,2,3], targetSum = 5 \texttt{root = [1,2,3], targetSum = 5} root = [1,2,3], targetSum = 5
输出: [] \texttt{[]} []
示例 3:
输入: root = [1,2], targetSum = 0 \texttt{root = [1,2], targetSum = 0} root = [1,2], targetSum = 0
输出: [] \texttt{[]} []
数据范围
- 树中结点数目在范围 [0, 5000] \texttt{[0, 5000]} [0, 5000] 内
- -1000 ≤ Node.val ≤ 1000 \texttt{-1000} \le \texttt{Node.val} \le \texttt{1000} -1000≤Node.val≤1000
- -1000 ≤ targetSum ≤ 1000 \texttt{-1000} \le \texttt{targetSum} \le \texttt{1000} -1000≤targetSum≤1000
前言
这道题是「路径总和」的进阶,要求返回所有的结点值总和等于目标和的从根结点到叶结点的路径。这道题也可以使用深度优先搜索和广度优先搜索得到答案,在搜索过程中需要维护路径。
解法一
思路和算法
如果二叉树为空,则不存在结点值总和等于目标和的路径。只有当二叉树不为空时,才可能存在结点值总和等于目标和的路径,需要从根结点开始寻找路径。
从根结点开始深度优先搜索,在遍历每一个结点的同时需要维护从根结点到当前结点的路径以及剩余目标和,将原目标和减去当前结点值即可得到剩余目标和。当访问到叶结点时,如果剩余目标和为 0 0 0,则从根结点到当前叶结点的路径即为结点值总和等于目标和的路径,将该路径添加到结果列表中。
由于深度优先搜索过程中维护的路径会随着访问到的结点而变化,因此当找到结点值总和等于目标和的路径时,需要新建一个路径对象添加到结果列表中,避免后续搜索过程中路径变化对结果造成影响。
代码
class Solution {List<List<Integer>> paths = new ArrayList<List<Integer>>();List<Integer> path = new ArrayList<Integer>();public List<List<Integer>> pathSum(TreeNode root, int targetSum) {dfs(root, targetSum);return paths;}public void dfs(TreeNode node, int targetSum) {if (node == null) {return;}path.add(node.val);targetSum -= node.val;if (node.left == null && node.right == null && targetSum == 0) {paths.add(new ArrayList<Integer>(path));}dfs(node.left, targetSum);dfs(node.right, targetSum);path.remove(path.size() - 1);}
}
复杂度分析
-
时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是二叉树的结点数。每个结点都被访问一次,最坏情况下每次将路径添加到结果中的时间是 O ( n ) O(n) O(n),因此总时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是递归调用的栈空间以及深度优先搜索过程中存储路径的空间,取决于二叉树的高度,最坏情况下二叉树的高度是 O ( n ) O(n) O(n)。注意返回值不计入空间复杂度。
解法二
思路和算法
使用广度优先搜索寻找结点值总和等于目标和的路径时,首先找到这些路径对应的叶结点,然后得到从叶结点到根结点的路径,将路径翻转之后即可得到相应的路径。
为了得到从叶结点到根结点的路径,需要使用哈希表存储每个结点的父结点,在广度优先搜索的过程中即可将每个结点和父结点的关系存入哈希表中。
广度优先搜索需要维护两个队列,分别存储结点与对应的结点值总和。广度优先搜索的过程中,如果遇到一个叶结点对应的结点值总和等于目标和,则找到一条结点值总和等于目标和的路径,利用哈希表中存储的父结点信息得到从当前叶结点到根结点的路径,然后将路径翻转,添加到结果中。
代码
class Solution {List<List<Integer>> paths = new ArrayList<List<Integer>>();Map<TreeNode, TreeNode> parents = new HashMap<TreeNode, TreeNode>();public List<List<Integer>> pathSum(TreeNode root, int targetSum) {if (root == null) {return paths;}Queue<TreeNode> nodeQueue = new ArrayDeque<TreeNode>();Queue<Integer> sumQueue = new ArrayDeque<Integer>();nodeQueue.offer(root);sumQueue.offer(root.val);while (!nodeQueue.isEmpty()) {TreeNode node = nodeQueue.poll();int sum = sumQueue.poll();TreeNode left = node.left, right = node.right;if (left == null && right == null && sum == targetSum) {paths.add(getPath(node));}if (left != null) {parents.put(left, node);nodeQueue.offer(left);sumQueue.offer(sum + left.val);}if (right != null) {parents.put(right, node);nodeQueue.offer(right);sumQueue.offer(sum + right.val);}}return paths;}public List<Integer> getPath(TreeNode node) {List<Integer> path = new ArrayList<Integer>();while (node != null) {path.add(node.val);node = parents.get(node);}Collections.reverse(path);return path;}
}
复杂度分析
-
时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是二叉树的结点数。每个结点都被访问一次,最坏情况下每次将路径添加到结果中的时间是 O ( n ) O(n) O(n),因此总时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是哈希表和队列空间,哈希表需要存储每个结点的父结点,需要 O ( n ) O(n) O(n) 的空间,两个队列内元素个数都不超过 n n n。注意返回值不计入空间复杂度。
