云南高端网站制作价格什么是sem和seo

二叉排序树（Binary Sort Tree）又称为二叉搜索树，二叉查找树，）

【算法思想】
（1）若二叉排序树为空，则查找失败，返回空指针。
（2）若二叉排序树非空，将给定值key与根结点的关键字T->data.key进行比较：
①若key等于T->data.key，则查找成功，返回根结点地址；
②若key小于T->data.key，则进一步查找左子树。
③若key大于T->data.key，则进一步查找右子树。
二叉排序树的定义：

typedef struct {KeyType key;//关键字项
};typedef struct BSTNode {ElemType data;struct BSTNode* lchild, * rchild;//左右孩子指针
}BSTNode,*BSTree;

二叉排序树的递归查找：

BSTree SearchBST(BSTree T, KeyType key) {//在根指针T所指向的二叉排序树中递归的查找关键字key的数据元素。//若查找成功，则返回指向该元素的指针，否则返回空指针。if ((!T) || key == T->data) {return T;}else if(key<T->data){ return SearchBST(T->lchild,key);}else {return SearchBST(T->rchild, key);}
}

二叉树的查找分析

二叉排序树上查找某关键字等于给定值的结点的过程，其实就是走了一条从根到该结点的路径。
比较的关键次数=该结点的层次数=最多的比较次数=树的深度

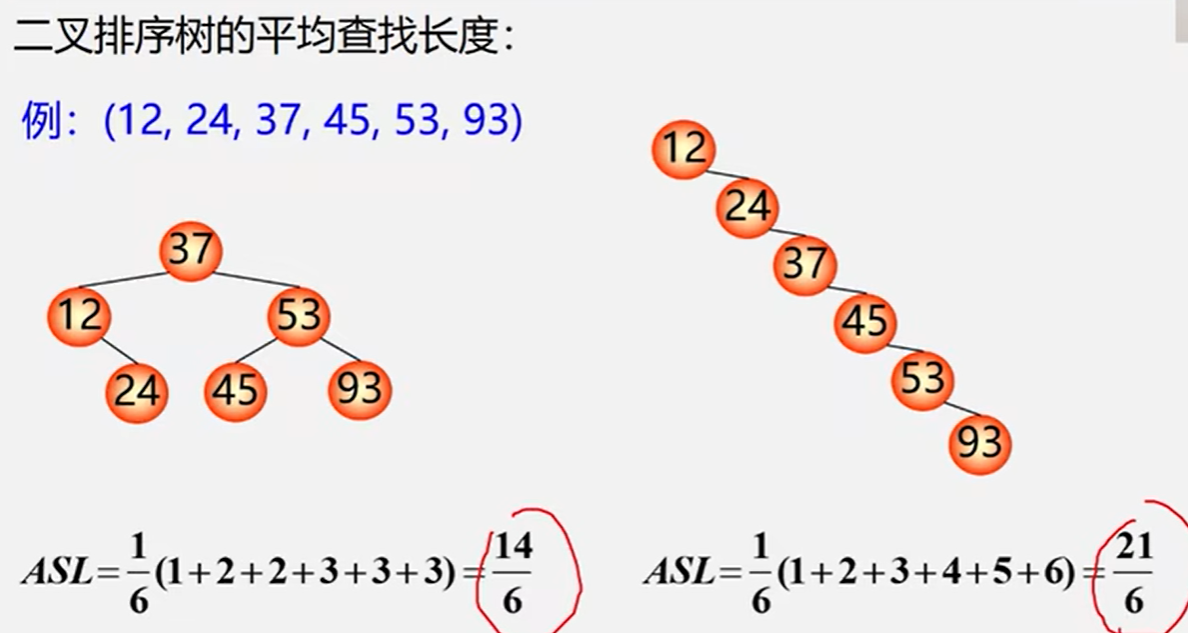
含有n个结点的二叉排序树的平均查找长度和树的形态有关。
如何提高形态不均衡的二叉排序树的查找效率？
做“平衡化”处理，即尽量的让二叉树的形态均衡。----->平衡二叉树。

二叉排序树的操作----插入

• 若二叉排序树为空，则插入结点作为根结点到空树中。
• 否则，继续在其左，右子树上查找。
  • 树中已有，不再插入。
  • 树中没有
  • 查找直至某个叶子结点的左子树或右子树为空，则插入结点应为叶子结点的左孩子或右孩子。

void InsertBST(BSTree& T, ElemType e) {if (!T) {BSTree S;S = new BSTNode;S->data = e;S->lchild = S->rchild = NULL;//新结点*S作为叶子结点T = S;}else if (T->data > e) {InsertBST(T->lchild, e);//将*S插入左子树}else if(T->data < e){InsertBST(T->rchild, e);//将*S插入右子树}
}

【算法分析】
二叉排序树的基本过程是查找，所以时间复杂度同查找一样，是O(log2n),2是底数。

二叉排序树的操作----生成

从空树出发，经过一系列的查找，插入操作之后，可生成某一棵二叉排序树。

一个无序序列可通过构造二叉排序树而变成一个有序序列。构造树的过程就是对无序序列进行排序的过程。
插入的结点均为叶子结点，故无需移动其他结点。
关键字的顺序不同，建立的不同二叉排序树。

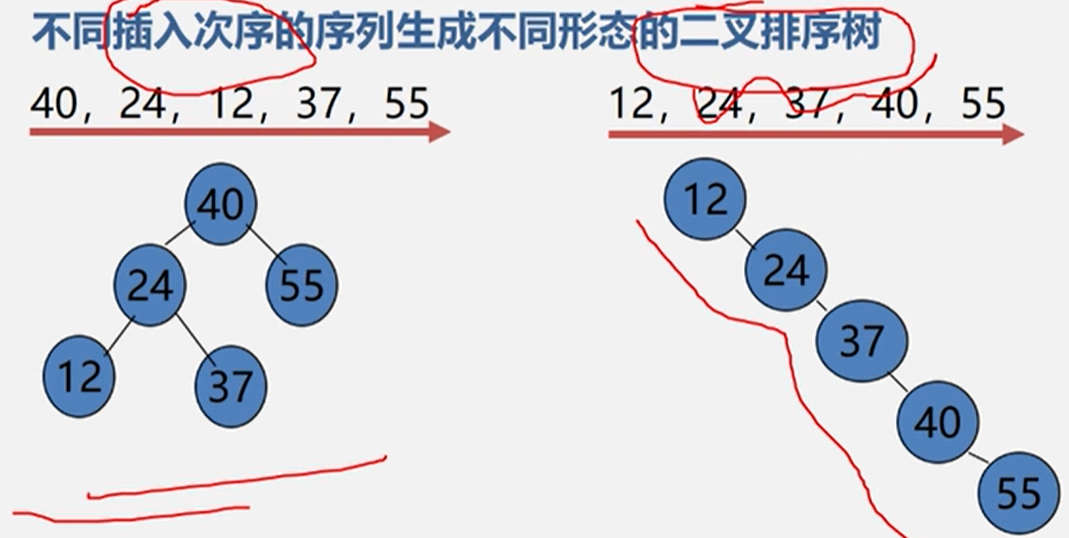
void CreateBST(BSTree& T) {//一次读入关键字为key的结点，将相应的节点插入到二叉排序树T中T = NULL;int e;cin >> e;int ENDFLAG = 0;while (T->data != ENDFLAG) {InsertBST(T, e);//将此结点插入到二叉排序树中去cin >> e;}
}

【算法分析】
假设有n个结点，则需要n次插入操作，而插入一个结点的算法的时间复杂度O（nlog2n），2为底数。

二叉排序树的操作----删除

（1）被删除的结点是叶子结点：直接删去该结点。
其双亲结点中相应的指针域的值改为“空”。
（2）被删除的结点只有左子树或者右子树，用其左子树或右子树替换它。（结点替换）。
其双亲结点相应的指针域的值改为“指向被删除结点的左子树或者右子树”。
（3）被删除的结点既有左子树，又有左子树。
- 以其中序前驱值替换之（值替换），然后再删除该前驱结点。前驱是左子树中最大的结点。

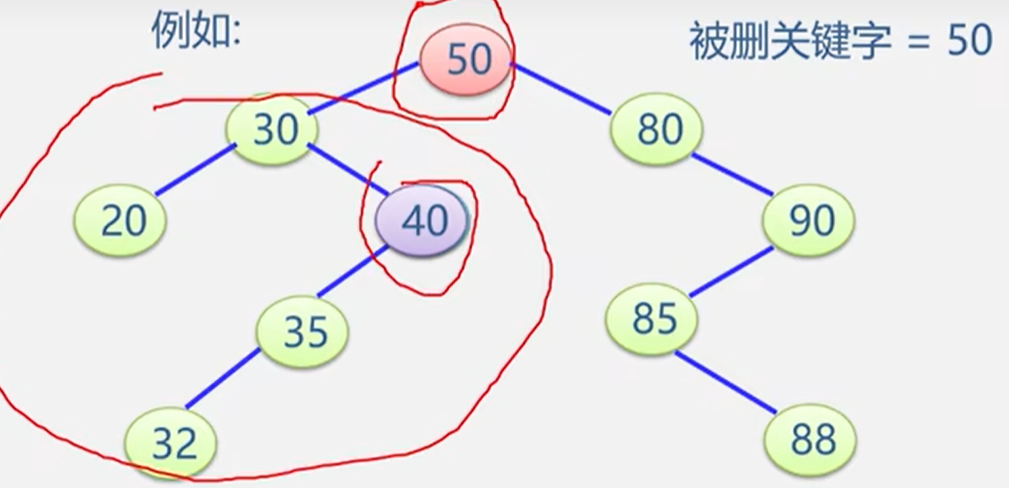
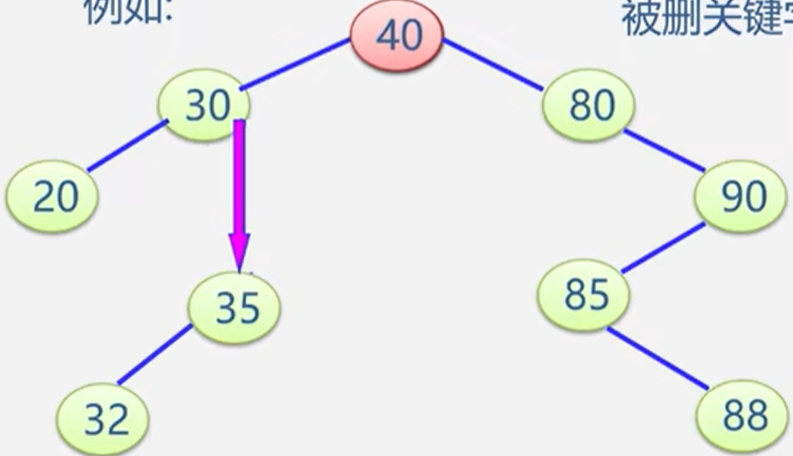
void DeleteBST(BSTree& T, KeyType key) {//从二叉排序树中删除关键字等于key的结点BSTree p = T;BSTree q,s;BSTree f = NULL;//初始化//下面的while循环是从根结点开始找key的遍历过程while (p) {if (p->data == key) {break;}else if (p->data > key) {p = p->lchild;}else {p = p->rchild;}}if (!p) {return;}q = p;if ((p->lchild) && (p->rchild)){//若被删的结点的左子树，右子树都不为空s = p->lchild;//在*p的左子树继续查找其前驱结点，即最右下结点while (s->rchild){q = s; s = s->rchild;//向右到尽头}p->data = s->data;//s指向被删结点的前驱if (q != p) {q->rchild = s->rchild;//重接*q的右子树}else {q->lchild = s->lchild;//重接*q的左子树}delete s;return;}else if (!p->rchild) {p = p->lchild;//被删结点*p无右子树，只需接起左子树}else if (!p->lchild) {p = p->rchild;//被删结点*p无左子树，只需接起右子树}if (!f) {T = p;//被删结点的为根结点}else if (q == f->lchild) {f->lchild = p;//挂接到*f的左子树位置}else {f->rchild = p;//挂接到*f的右子树位置}delete q;
}

总代码

#include<iostream>
using namespace std;#define KeyType int
#define ElemType inttypedef struct {KeyType key;//关键字项
};typedef struct BSTNode {ElemType data;struct BSTNode* lchild, * rchild;//左右孩子指针
}BSTNode,*BSTree;BSTree SearchBST(BSTree T, KeyType key) {//在根指针T所指向的二叉排序树中递归的查找关键字key的数据元素。//若查找成功，则返回指向该元素的指针，否则返回空指针。if ((!T) || key == T->data) {return T;}else if(key<T->data){ return SearchBST(T->lchild,key);}else {return SearchBST(T->rchild, key);}
}void InsertBST(BSTree& T, ElemType e) {if (!T) {BSTree S;S = new BSTNode;S->data = e;S->lchild = S->rchild = NULL;//新结点*S作为叶子结点T = S;}else if (T->data > e) {InsertBST(T->lchild, e);//将*S插入左子树}else if(T->data < e){InsertBST(T->rchild, e);//将*S插入右子树}
}void CreateBST(BSTree& T) {//一次读入关键字为key的结点，将相应的节点插入到二叉排序树T中T = NULL;int e;cin >> e;int ENDFLAG = 0;while (T->data != ENDFLAG) {InsertBST(T, e);//将此结点插入到二叉排序树中去cin >> e;}
}void DeleteBST(BSTree& T, KeyType key) {//从二叉排序树中删除关键字等于key的结点BSTree p = T;BSTree q,s;BSTree f = NULL;//初始化//下面的while循环是从根结点开始找key的遍历过程while (p) {if (p->data == key) {break;}else if (p->data > key) {p = p->lchild;}else {p = p->rchild;}}if (!p) {return;}q = p;if ((p->lchild) && (p->rchild)){//若被删的结点的左子树，右子树都不为空s = p->lchild;//在*p的左子树继续查找其前驱结点，即最右下结点while (s->rchild){q = s; s = s->rchild;//向右到尽头}p->data = s->data;//s指向被删结点的前驱if (q != p) {q->rchild = s->rchild;//重接*q的右子树}else {q->lchild = s->lchild;//重接*q的左子树}delete s;return;}else if (!p->rchild) {p = p->lchild;//被删结点*p无右子树，只需接起左子树}else if (!p->lchild) {p = p->rchild;//被删结点*p无左子树，只需接起右子树}if (!f) {T = p;//被删结点的为根结点}else if (q == f->lchild) {f->lchild = p;//挂接到*f的左子树位置}else {f->rchild = p;//挂接到*f的右子树位置}delete q;
}int main() {return 0;
}```