网站建设_广告关键词排名

一个系统中事件发生的概率越大，也就是其确定性越大，则其包含的信息量越少，可以认为一个事件的信息量就是该事件发生难度的度量，事件所包含的信息量越大则其发生的难度越大。并且相互独立的事件，信息量具有可加性。相互独立的事件的概率具有可乘性，为了使得概率的这种相乘可以和信息量的累加相匹配，所以给事件的概率加上负对数(或者叫做概率倒数的对数)，用来定义信息量，而一个系统的平均信息量就叫做这个系统的熵(也叫信息熵)，换句话说，一个系统的熵就是这个系统中事件信息量的期望。其中所谓的系统，其实就是包含了一系列随机事件，且随机事件的概率总和为1，在概率论中其实就是我们常说的概率分布。从上可以看出，熵也就是一种特殊的信息量，特殊的地方在于熵只能用来描述系统，而不能用来描述单独的事件。当信息量中的对数的底为2时(其实信息熵是源中的信息量的加权平均，对数的底是默认源中符号总数。一般通信中用到都是bsc(二元对称信道)，所以默认取r=2)，也称信息熵为理论最小平均编码长度，单位是比特。
具体见下图，其中P为概率分布，H§为分布P的信息熵，:=符号为定义符号，相比于=更加准确，E(Pf)为分布P中所有事件信息量的期望，pi为系统P中某个事件的概率，f(pi)为该事件的信息量。

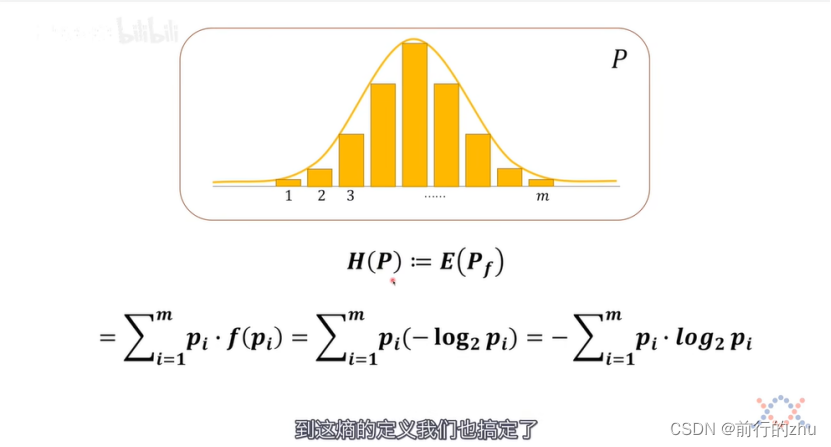
从上可知，可以知道如下的定义推导，事件的概率–>事件的信息量–>概率分布的熵；
需要注意的是，对于同一个事件，其在不同分布出现的概率可能不同，所以对应的信息量也可能不同，记住这一点，在后面将交叉熵的时候有用。
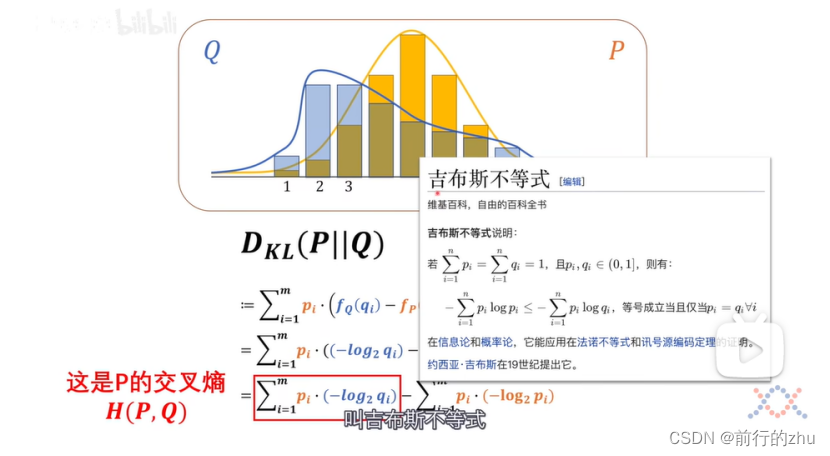
接下来我们来看看相对熵(更常见的叫法是kl散度)，为了更加易于理解，下文都叫相对熵，相对熵其实就是度量两个分布熵的差异，既然是比较，那么就需要有一个基准，对于如下的式子DKL(P||Q),就是以P分布为基准，Q分布相对于P分布的相对熵。也可以认为，分布Q距离分布P还需要多少信息量，如果通过某种操作，比如调整分布Q的参数和类型等，将所差的信息量补齐(就是相对熵为0)，那么分布Q将和分布P完全一样。具体公式如下：

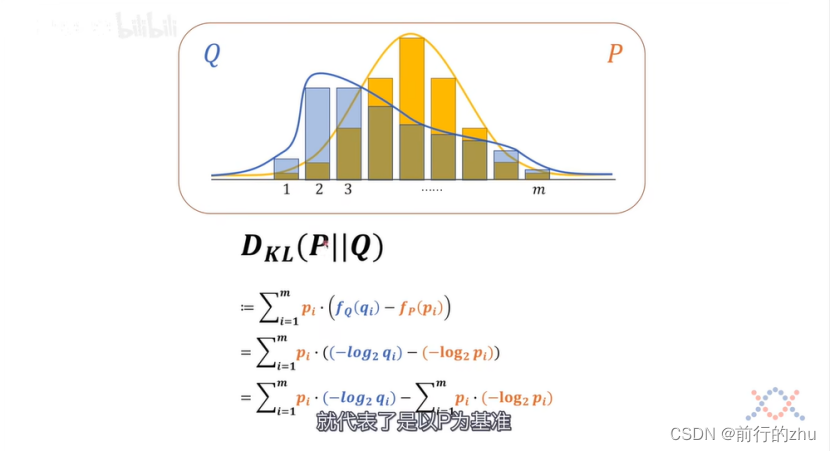
其中，pi为基准分布P中某个事件的概率，fQ(qi)为上述事件在分布Q中的信息量，fp(pi)为上述事件在分布P中的信息量。上述式子经过展开后

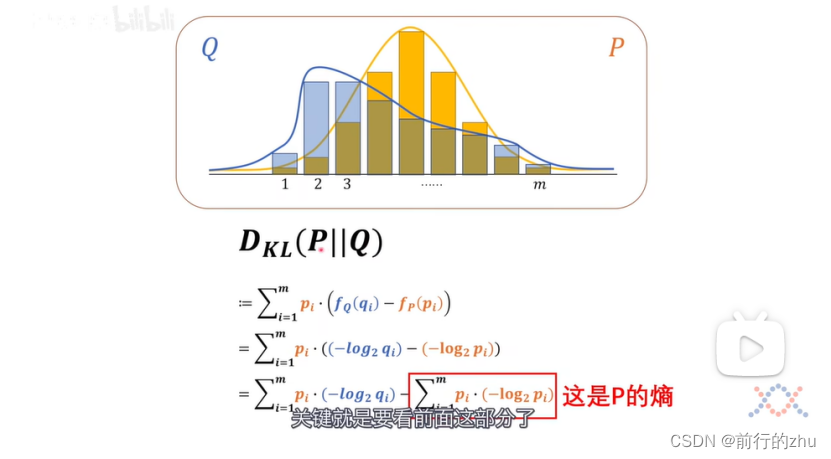
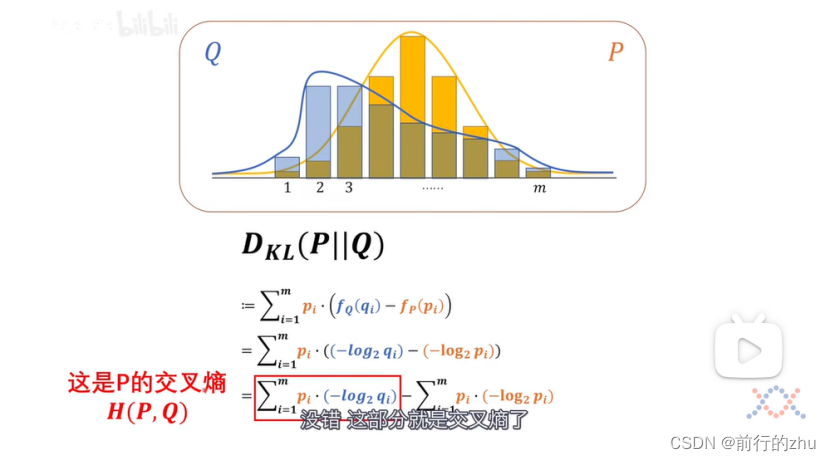
可以看到所谓相对熵其实就等于两个分布的交叉熵减去基准分布的熵。交叉熵为H(P,Q),为P分布和Q分布的交叉熵，为所有基准分布件的概率和该事件在比较分布中对应的信息量的乘积之和。还记得我们上文说的，同一个事件在不同的分布中的概率和信息量可能不同吗？如果任何一个事件在两个分布中的概率和信息量都一样，也就是对于所有的i，pi和qi都一样，则上面式子中的交叉熵H(P,Q)就和基准分布P的熵H(P一样了，也即P和Q的相对熵为0，此时分布P和Q完全一样。
需要注意的是根据吉布斯不等式，两个分布的交叉熵一定大于等于任何一个分布的熵，仅当两个分布一样时等号成立；

另一个是交叉熵不是对称的，也就是H(P,Q)不等于H(Q,P)，同理相对熵也是不对称的。
我们在真实的机器学习算法求损失函数时，实际是以真实分布为基准分布P，我们估计的分布为比较分布Q来计算相对熵，相对熵就是两个分布的“距离”,所以我们使用数据训练模型的目的就是尽可能的使我们的估计分布Q来更接近真实分布P，也就是让相对熵尽可能的小。对于上述相对熵的公式进行求导(对Q分布的参数θ)时，由于真实分布P和θ无关，所以其导数为0，于是便出现了相对熵对θ的导数等于了交叉熵对θ的导数。这也就是我们常说的交叉熵损失函数。
强烈建议结合b站up主的视频进行理解：
“交叉熵”如何做损失函数？打包理解“信息量”、“比特”、“熵”、“KL散度”
【10分钟】了解香农熵，交叉熵和KL散度