龙岩kk网手机版杭州网络优化公司排名
一. 初识算法
1.1 什么是算法?
在数学和计算机科学领域,算法是一系列有限的严谨指令,通常用于解决一类特定问题或执行计算
不正式的说,算法就是任何定义优良的计算过程:接收一些值作为输入,在有限的时间内,产生一些值作为输出。
1.2 什么是数据结构?
在计算机科学领域,数据结构是一种数据组织、管理和存储格式,通常被选择用来高效访问数据
数据结构是一种存储和组织数据的方式,旨在便于访问和修改
1.3 衡量算法好坏
一般从以下维度来评估算法的优劣:正确性、可读性、健壮性(对不合理输入的反应能力和处理能力)。
时间复杂度(time complexity):估算程序指令的执行次数(执行时间)。
空间复杂度(space complexity):估算所需占用的存储空间。
1.3.1 时间复杂度
常见的时间复杂度从快到慢:
常数复杂度 O(1)
对数复杂度 O(logn)
线性时间复杂度 O(n)
线性对数复杂度 O(nlogn)
平方 O(
)
立方 O(
)
指数 O(
)
阶乘 O(n!)
1.3.2 空间复杂度
空间复杂度就是算法需要多少内存,占用了多少空间
常用的空间复杂度有O(1)、O(n)、O()
二、二分查找
二分查找算法也称折半查找,是一种非常高效的工作于有序数组的查找算法。
2.1 二分查找基础版


/*** @description: 二分查找基础版* @author: 憨憨浩浩* @date: 2023/12/11 21:54* @param: [a, target]* @return: int**/public static int binarySearchBasic(int[] a, int target) {// 定义左侧指针int i = 0;// 定义右侧指针int j = a.length - 1;// 当 i > j 时退出循环while (i <= j){// 定义中间指针int m = (i + j) / 2;if (a[m] > target){ // 目标值在左边j = m - 1;}else if (a[m] < target){ // 目标值在右边i = m + 1;}else { // 找到目标值返回对应索引return m;}}return -1; // 找不到目标值返回-1}
(i + j) / 2 有没有问题?
有问题,当数组长度足够长是会发生问题;
@Testpublic void Test01(){int i = Integer.MAX_VALUE / 2;int j = Integer.MAX_VALUE;int m = (i + j) / 2;System.out.println(m); // -536870913}解决方案:
@Testpublic void Test02(){int i = Integer.MAX_VALUE / 2;int j = Integer.MAX_VALUE;int m = (i + j) >>> 2;System.out.println(m); // 805306367}2.2 二分查找改变版
另一种写法
/*** @description: 二分查找改变版* @author: 憨憨浩浩* @date: 2023/12/11 22:10* @param: [a, target]* @return: int**/public static int binarySearchAlternative(int[] a,int target){// 定义左侧指针int i = 0;// 定义右侧指针int j = a.length;// 当 i = j 时退出循环while (i < j){// 定义中间指针int m = (i + j) /2;if (a[m] > target){ // 目标值在左边j = m;} else if (a[m] < target) { // 目标值在右边i = m + 1;}else { // 找到目标值返回对应索引return m;}}return -1; // 找不到目标值返回-1}
2.3 二分查找性能

2.4 二分查找平衡版
/*** @description: 二分查找平衡版* @author: 憨憨浩浩* @date: 2023/12/13 13:46* @param: [a, target]* @return: int**/public static int binarySearchBalance(int[] a,int target){// 定义左侧指针int i = 0;// 定义右侧指针int j = a.length;// 当 i + 1 > j 时退出循环while (1 < j - i) {// 定义中间指针int m = (i + j) >>> 1;if (target < a[m]) { // 目标值在左边j = m;} else {i = m;}}// 查到返回i,查不到返回-1return (a[i] == target) ? i : -1;}
2.5 二分查找 Java 版
Java8源码:

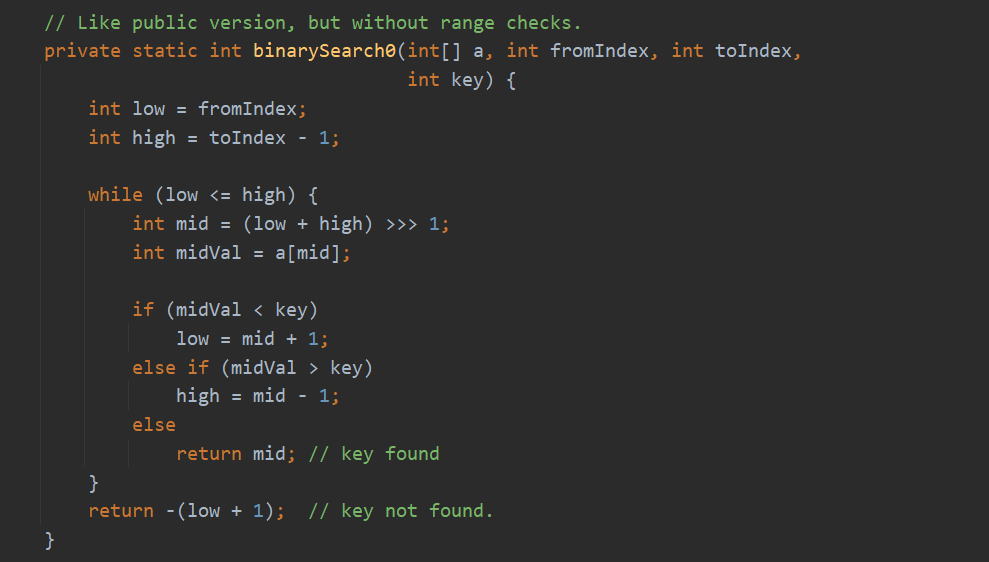
public static int binarySearch(int[] a, int key) {return binarySearch0(a, 0, a.length, key);}private static int binarySearch0(int[] a, int fromIndex, int toIndex, int key) {int low = fromIndex;int high = toIndex - 1;while (low <= high) {int mid = (low + high) >>> 1;int midVal = a[mid];if (midVal < key)low = mid + 1;else if (midVal > key)high = mid - 1;elsereturn mid; // key found}return -(low + 1); // key not found.}
2.6 Leftmost 与 Rightmost

/*** @description: 二分查找返回左侧的索引值* @author: 憨憨浩浩* @date: 2023/12/15 20:21* @param: [a, target]* @return: int**/public static int binarySearchLeftmost1(int[] a,int target){int i = 0, j = a.length - 1;int candidate = -1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) {j = m - 1;} else if (a[m] < target) {i = m + 1;} else {candidate = m; // 记录候选位置j = m - 1; // 继续向左}}return candidate;}如果希望返回的是最右侧元素
/*** @description: 二分查找返回最右侧值的索引* @author: 憨憨浩浩* @date: 2023/12/15 20:23* @param: [a, target]* @return: int**/public static int binarySearchRightmost1(int[] a,int target){int i = 0, j = a.length - 1;int candidate = -1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) {j = m - 1;} else if (a[m] < target) {i = m + 1;} else {candidate = m; // 记录候选位置i = m + 1; // 继续向右}}return candidate;}应用
对于 Leftmost 与 Rightmost,可以返回一个比 -1 更有用的值
Leftmost 改为
public static int binarySearchLeftmost(int[] a, int target) {int i = 0, j = a.length - 1;while (i <= j) {int m = (i + j) >>> 1;if (target <= a[m]) {j = m - 1;} else {i = m + 1;}}return i;
}
Rightmost 改为
public static int binarySearchRightmost(int[] a, int target) {int i = 0, j = a.length - 1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) {j = m - 1;} else {i = m + 1;}}return i - 1;
}大于等于中间值,都要向右找
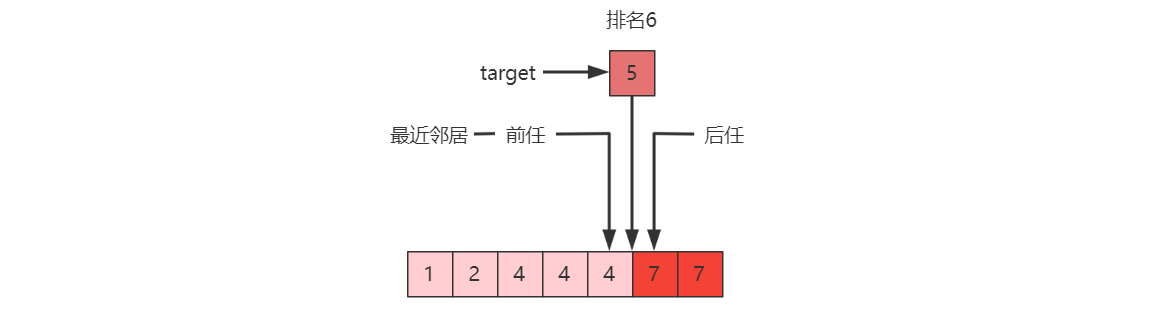
几个名词