网站做电话线用怎么做电商生意

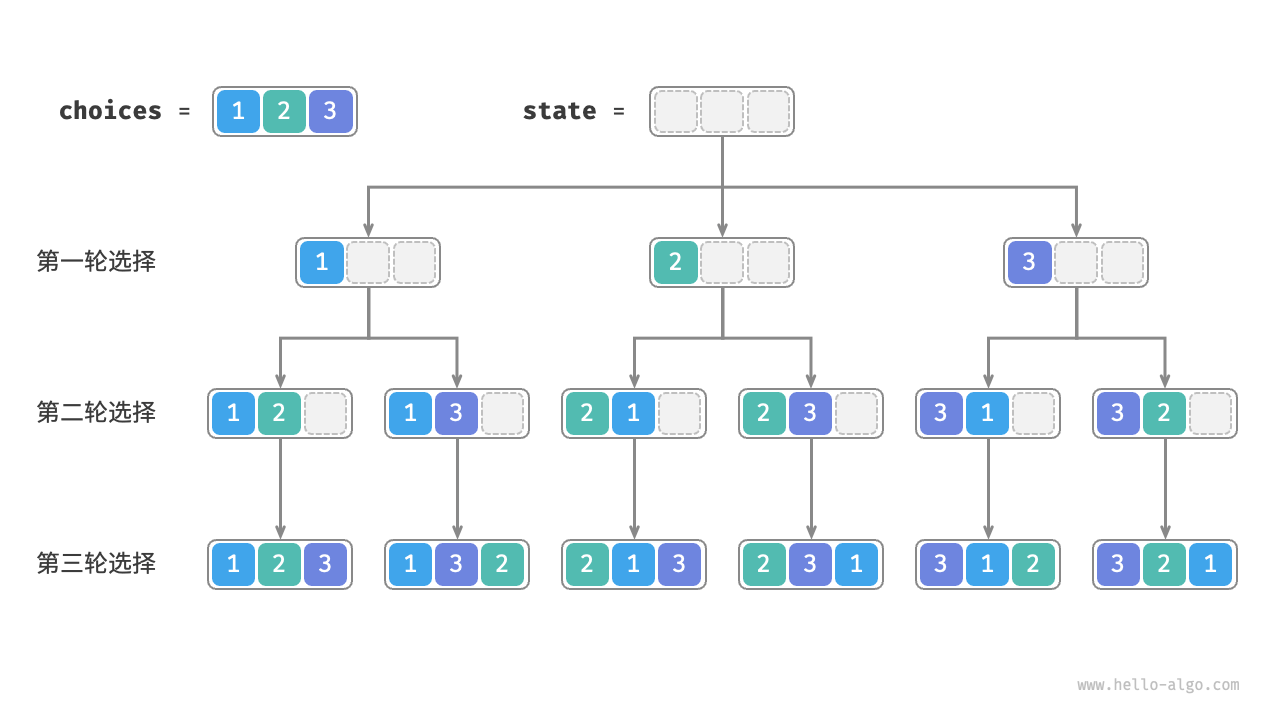
全排列问题

• 数字序列$[l,r]$​区间内元素的全排列问题

extern int ans[],l,r,num;//num：方案数
extern bool flag[];
void dfs(int cl){//cl:current left，即为当前递归轮的首元素if(cl == r + 1){//数组已越界，本轮递归结束for(int i=l;i<=r;i++) cout<<ans[i];//从区间头开始扫描并输出cout<<endl;num++;return;}for(int i=l;i<=r;i++){//if(!flag[i]){//剪枝:不允许重复选择已被选择的元素flag[i]=1,ans[cl]=i;dfs(cl + 1);flag[i]=0;//回溯}}
}

• 数组索引$[l,r]$​区间内元素的全排列问题

思路：

1. 让当前的首元素(索引为$cl$)不同，分割成$r$轮，(首元素相同的称为1轮，共$r$轮)
   方法：首元素和其之后每个元素交换 (for控制$r$轮广度)
2. 每轮中第$[l+1,r]$的元素分割出来小区间，令$cl=l+1$(对应dfs递归传参)，重复步骤1。
   方法：递归控制

extern int a[],l,r,num;//num:方案数
void dfs(int cl){//cl:current left，即为当前递归轮的首元素if(cl == r + 1){//数组已越界，本轮递归结束for(int i = l; i <= r; i++)//从用户输入区间头开始遍历输出cout << a[i];cout << endl;num++;return;}for(int i = cl; i <= r; i++){//从本轮递归区间头开始扫描 i=cl是因为数组本身也算是一种排列方案swap(a[cl], a[i]);//本轮递归区间首元素与其之后每个元素都互换dfs(cl + 1);swap(a[cl], a[i]);//回溯}
}

全组合问题

• $[l,r]$区间内组合问题

extern int n, l, r,ans[n];
void dfs(int k, int last) {//k:当前已选元素个数 last:上一轮递归中选择的元素值if (k == n + 1) {//k已越界，输出答案for (int i = 0; i < n; i++) cout<<ans[i]<<' ';cout<<endl;return;}for (int i = last + 1; i <= r; i++) {//从last+1开始是为了选择不会与上一轮递归重复ans[k - 1] = i;dfs(k + 1, i);}
}
int main() {//...dfs(1, l - 1); // 从l-1开始，确保l能被选中//...
}

子集问题