个人做网站排版广告网站推荐

【LetMeFly】2673.使二叉树所有路径值相等的最小代价：自顶向下的DFS 或 自底向上的递推

力扣题目链接：https://leetcode.cn/problems/make-costs-of-paths-equal-in-a-binary-tree/

给你一个整数 n 表示一棵 满二叉树 里面节点的数目，节点编号从 1 到 n 。根节点编号为 1 ，树中每个非叶子节点 i 都有两个孩子，分别是左孩子 2 * i 和右孩子 2 * i + 1 。

树中每个节点都有一个值，用下标从 0 开始、长度为 n 的整数数组 cost 表示，其中 cost[i] 是第 i + 1 个节点的值。每次操作，你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。

你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。

注意：

• 满二叉树 指的是一棵树，它满足树中除了叶子节点外每个节点都恰好有 2 个节点，且所有叶子节点距离根节点距离相同。
• 路径值 指的是路径上所有节点的值之和。

 

示例 1：

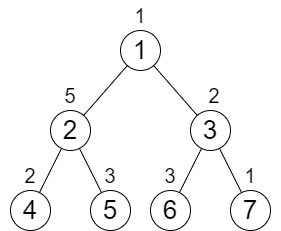
输入：n = 7, cost = [1,5,2,2,3,3,1]
输出：6
解释：我们执行以下的增加操作：
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。

示例 2：

输入：n = 3, cost = [5,3,3]
输出：0
解释：两条路径已经有相等的路径值，所以不需要执行任何增加操作。

 

提示：

• 3 <= n <= 105
• n + 1 是 2 的幂
• cost.length == n
• 1 <= cost[i] <= 104

思路

对于某个节点，假设其左子树和右子树都已经“增加”过了（对于左子树，所有路径值相等，右子树同理），但是左子树根到叶路径之和（记为leftSum）和右子树的rightSum不等，我们应该怎么操作呢？

举例说明点我

例如如下二叉树中

   15   2
2 3 3 1

的根节点1，假设其左子树已经由

 5
2 3

变成了

 5
3 3

，而右子树已经由

 2
3 1

变成了

 2
3 3

那么我们应该如何进行下一步操作呢？

对于根节点1：其左子树已经平衡，路径之和为5 + 3 = 8；其右子树已经平衡，路径之和为2 + 3 = 5。

想要让左右子路径之和相等？当然只要右子的根节点+3即可。

也就是说：

将左右子树路径和之差加到路径和较小的子树的根节点上。

这是因为“加一操作”越靠近根，所能影响的路径数就越多。

方法一：自顶向下的DFS

首先要说明的是这种方法的空间复杂度不如方法二，但是比方法二更容易理解。

我们只需要写一个函数dfs(n)返回节点n（根节点下标从0开始）为根到叶节点的路径之和：

1. 递归左子树得到leftSum，递归右子树得到rightSum

2. 将leftSum和rightSum之差累加到答案中

3. 返回max(leftSum, rightSum) + cost[n]作为该节点到叶节点的路径之和

终止条件：n超出数组范围

• 时间复杂度$O(N)$，其中$N$为二叉树节点个数。
• 空间复杂度$O(\log N)$，满二叉树的深度是$\log N$级别的。

AC代码

C++

class Solution {
private:int ans;int dfs(int n, vector<int>& cost) {if (n >= cost.size()) {return 0;}/*01   23 4 5 6*/int leftSum = dfs(n * 2 + 1, cost);int rightSum = dfs(n * 2 + 2, cost);ans += max(leftSum, rightSum) - min(leftSum, rightSum);return max(leftSum, rightSum) + cost[n];}
public:int minIncrements(int n, vector<int>& cost) {ans = 0;dfs(0, cost);return ans;}
};

方法二：自底向上的递推

在自顶向下的方法一中，递归占用了$O(N)$的空间复杂度。因为往下计算的过程中还要存储当前节点的信息。

因此我们可以倒过来，采用自底向上的方法：

1. 从最后一个非叶节点开始往根节点遍历

2. 这个节点的两个子节点之差累加到答案

3. 这个节点的两个子节点的最大值累加到这个节点（路径累加）

这样相当于是把值存放到$cost$数组中了。

• 时间复杂度$O(N)$，其中$N$为二叉树节点个数。
• 空间复杂度$O(1)$，但是我们修改了$cost$数组的值。若其值不能被修改，则空间复杂度为$O(N)$（大于方法一的$O(\log N)$，因为方法一底部的值向上传递后可以被丢弃）

AC代码

C++

class Solution {
public:int minIncrements(int n, vector<int>& cost) {int ans = 0;for (int i = n / 2 - 1; i >= 0; i--) {ans += abs(cost[i * 2 + 1] - cost[i * 2 + 2]);cost[i] += max(cost[i * 2 + 1], cost[i * 2 + 2]);}return ans;}
};

Python

# from typing import Listclass Solution:def minIncrements(self, n: int, cost: List[int]) -> int:ans = 0for i in range(n // 2 - 1, -1, -1):ans += abs(cost[i * 2 + 1] - cost[i * 2 + 2])cost[i] += max(cost[i * 2 + 1], cost[i * 2 + 2])return ans

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/136357361