做网站跟app需要多少钱黄页网络的推广网站有哪些软件

AVL树

理论

我们知道二叉搜索树拥有极高的搜索效率，但当二叉搜索树退化成单支时，其查找效率会大幅下降，因此我们需要避免其出现单支的情况，并且尽可能让其接近满二叉树。解决办法是每次插入一个新结点时，都要保证所有结点的左右子树高度差都不能超过1，倘若新结点插入导致某颗子树左右子树的高度差超过1，就需要进行旋转处理，这样处理后的树称之为AVL树，可以保证其高度不会过高，其查找的时间复杂度的数量级为log(n)。

我们需要在每一个结点中增加一个变量bf以记录该结点的左右子树高度差（称之为平衡因子，一般是用右子树高度减去左子树高度的差作为平衡因子，AVL树中其值只能为-1，0，1）。当我们插入的新结点时，需要对从插入结点到根结点路径上的平衡因子进行调整，调整方法为：左子树高度增加，则当前结点平衡因子减1，右子树高度增加，则当前结点平衡因子加1，接着对其父结点也进行以上操作，直至根结点或者某个祖先结点的平衡因子变为0为止（当前结点平衡因子变为0说明新结点的插入并不影响以当前结点为根的子树的高度，那么自然就不会影响其到根结点路径上的祖先结点的平衡因子）。
倘若调整平衡因子过程中某个结点g的平衡因子变为了-2或者2，则需要进行旋转处理以合理调整树的高度，旋转的情况分为以下4种：

①g的左孩子为p，新插入结点c在p的左子树中

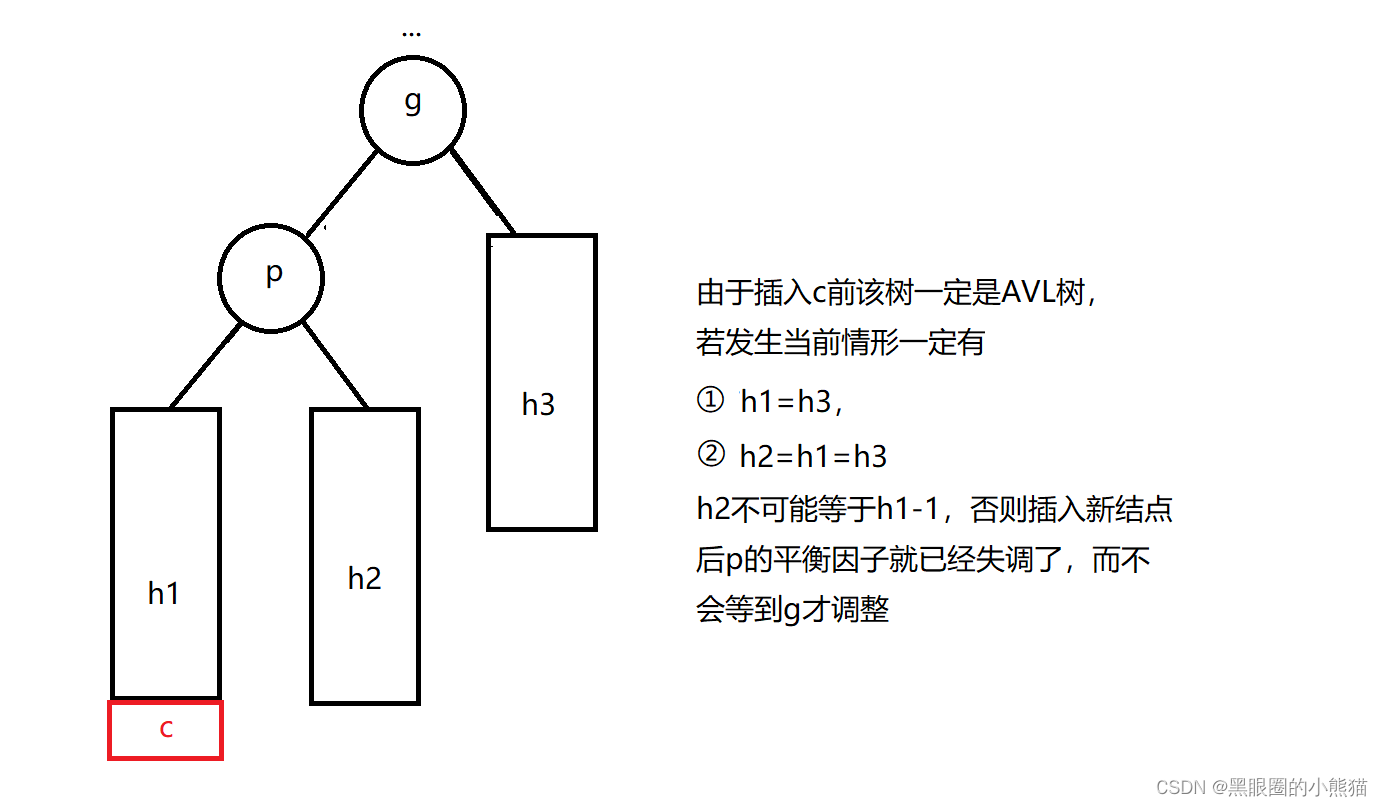
这种情况需要进行以g为根结点进行右单旋，具体步骤为：先将g的左孩子指向改为子树h2，h2子树的根结点的父亲指向改为指向g（如果子树h2存在的话），接着将p的左孩子指向改为指向g，p的父亲指向改为指向g指向的父结点，最后将g的父亲结点指向g的孩子指向改为指向p（如果g的父亲结点存在的话），g的父亲指向改为指向p。

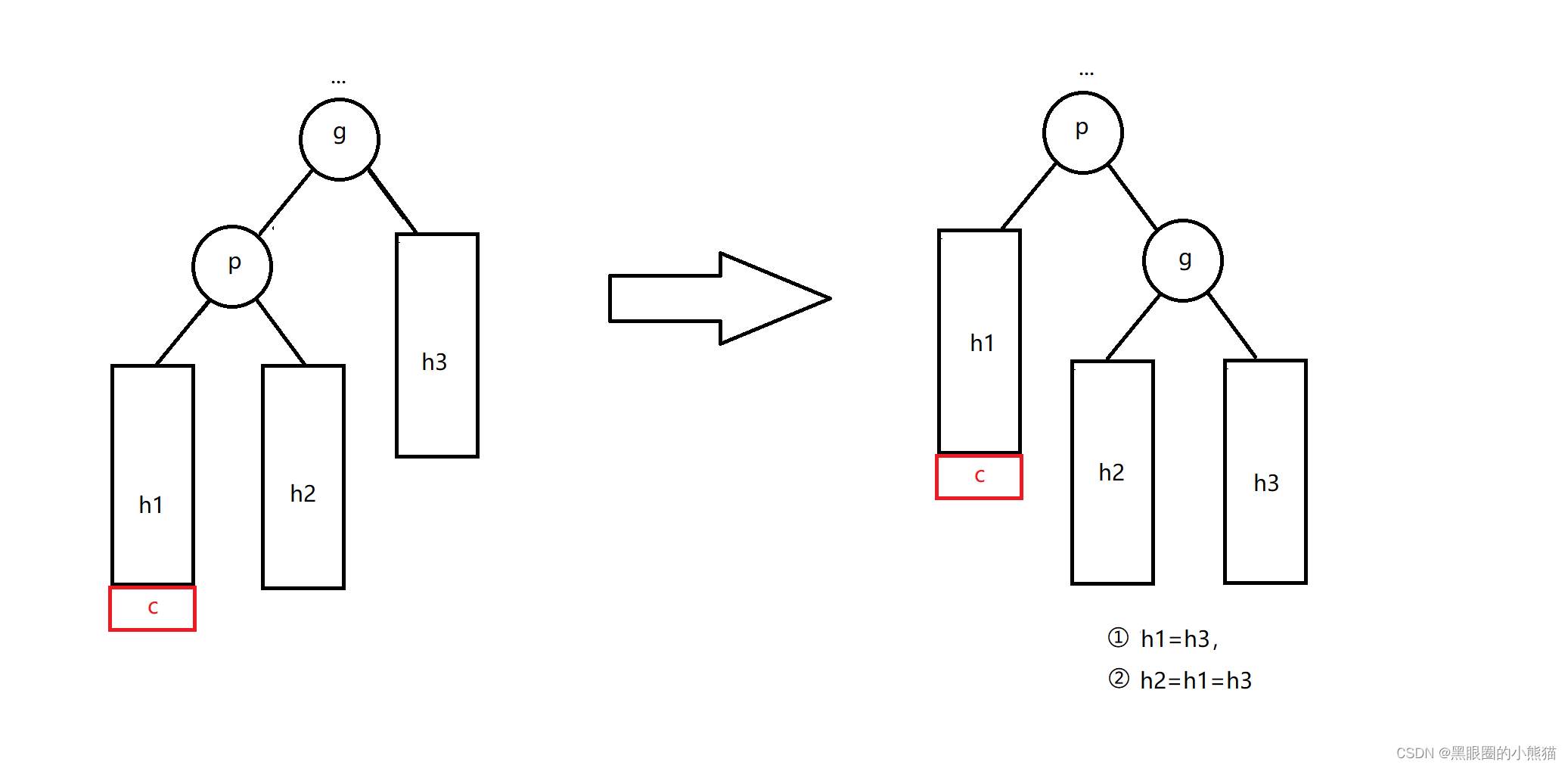
此时p的平衡因子必定为0，调整后以p为根结点的子树的高度与插入结点前以g为根结点的子树高度相比并无变化，因此从p结点到根结点路径上面的祖先结点的平衡因子不需要再进行调整。

②g的右孩子为p，新插入结点c在p的右子树中

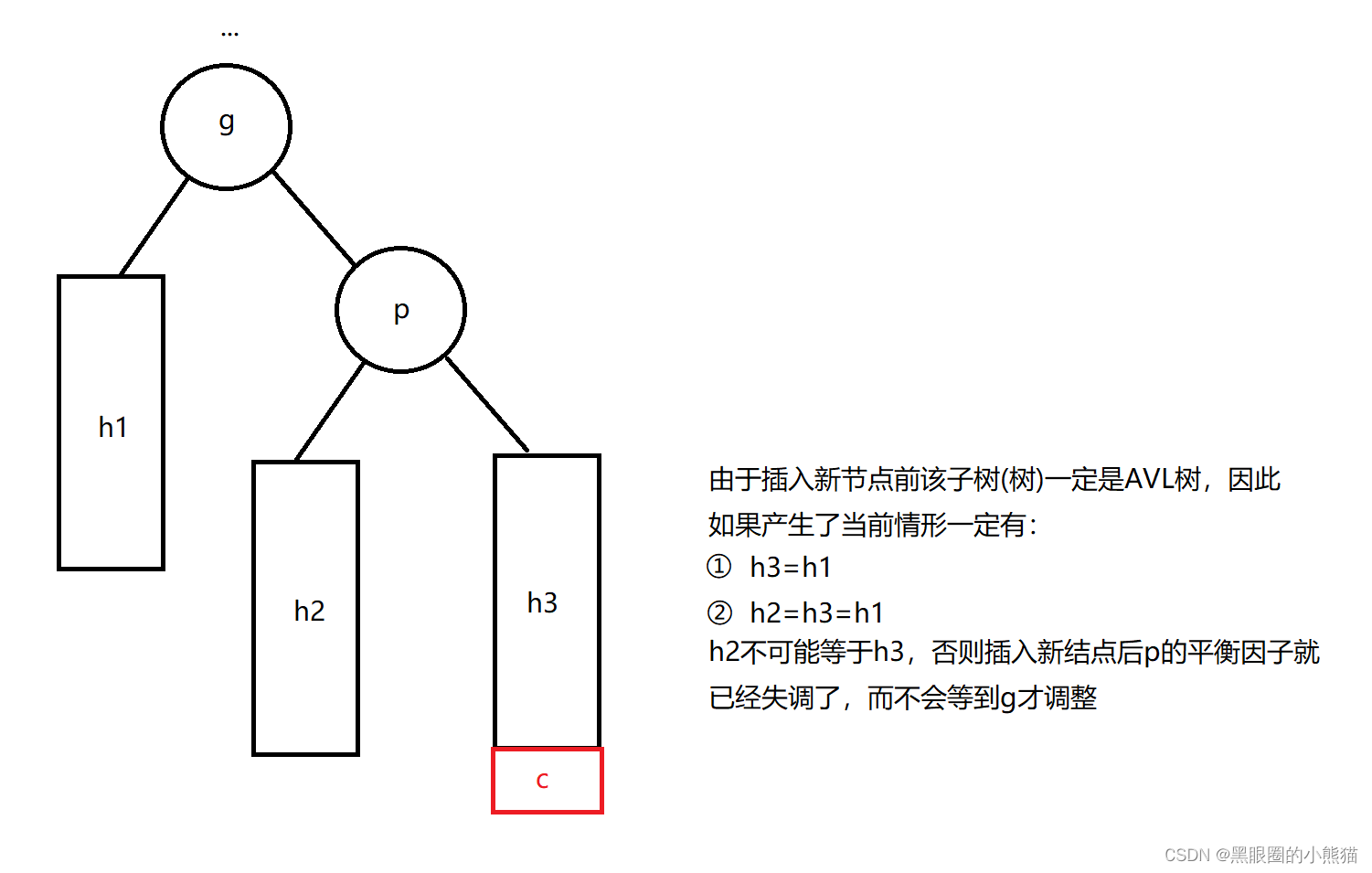
这种情况我们需要以g为根结点进行左单旋，具体步骤为：先将g的右孩子指向改为指向子树h2，再将h2的根结点的父亲指向改为指向g（如果子树h2不为空），接着将p的左孩子指向改为指向g，p的父亲指向改为指向g指向的父亲结点，最后将的父结点指向g的孩子指向改为指向p，g的父亲指向改为指向p。

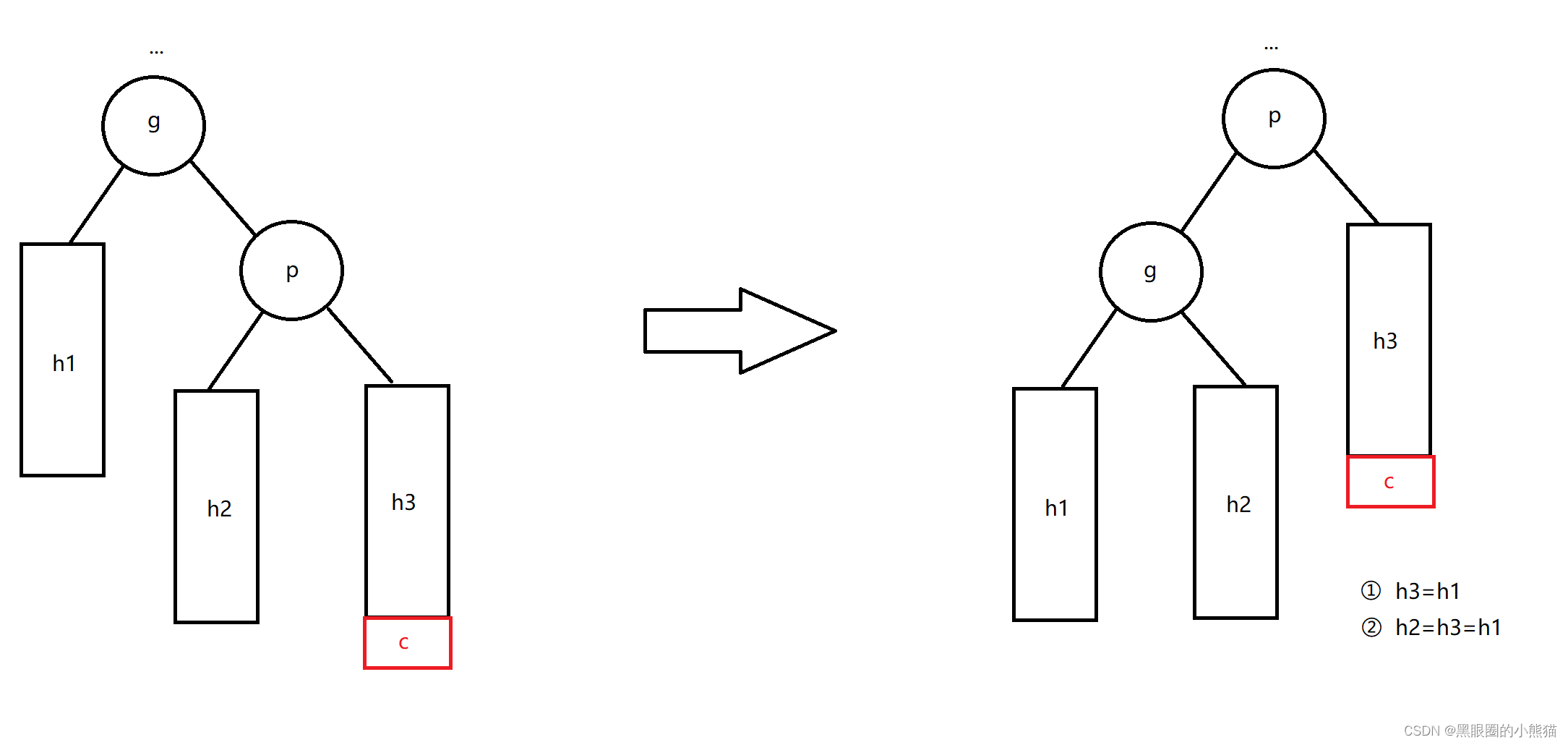
此时p的平衡因子也必定为0，调整后以p为根结点的子树的高度与插入结点前以g为根结点的子树高度相比也无变化，因此从p结点到根结点路径上面的祖先结点的平衡因子也不需要再进行调整。

③g的左孩子为p，新插入结点c在p的右子树中

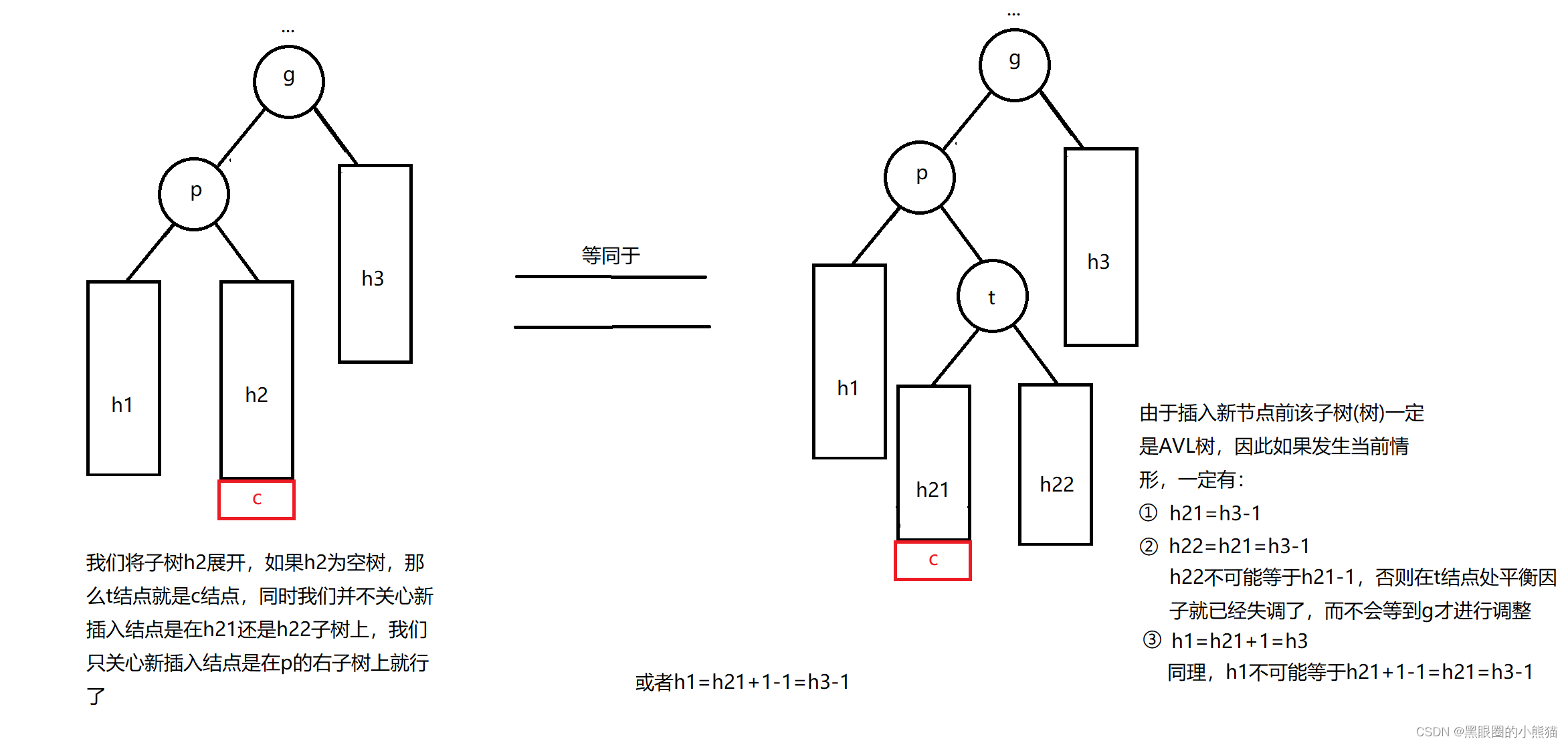
这种情况我们需要进行左右双旋，具体做法为：
1.以p结点为根结点进行左单旋
2.以g结点为根结点进行右单旋

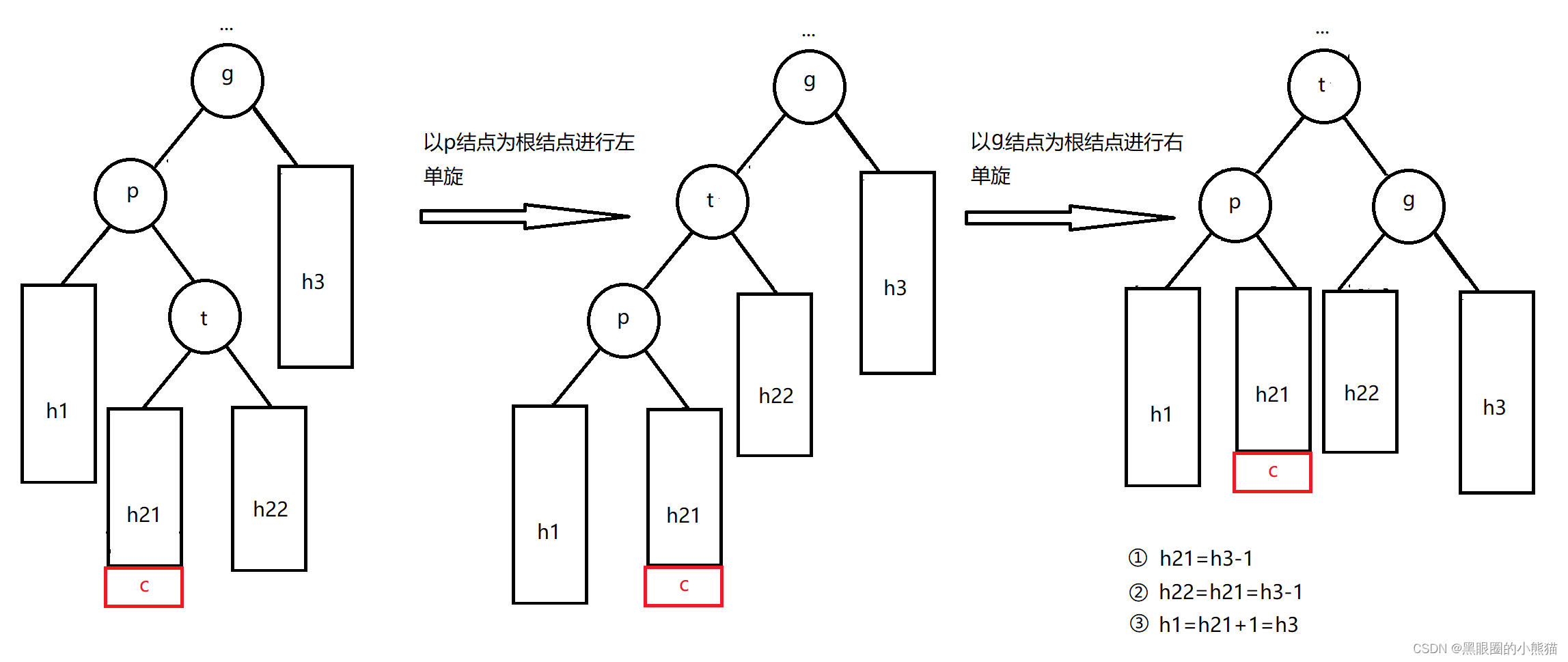
此时结点t的平衡因子也必定为0，调整后以p为根结点的子树的高度与插入结点前以g为根结点的子树高度相比并无变化，因此从p结点到根结点路径上面的祖先结点的平衡因子不需要再进行调整。

④g的右孩子为p，新插入结点c在p的左子树中

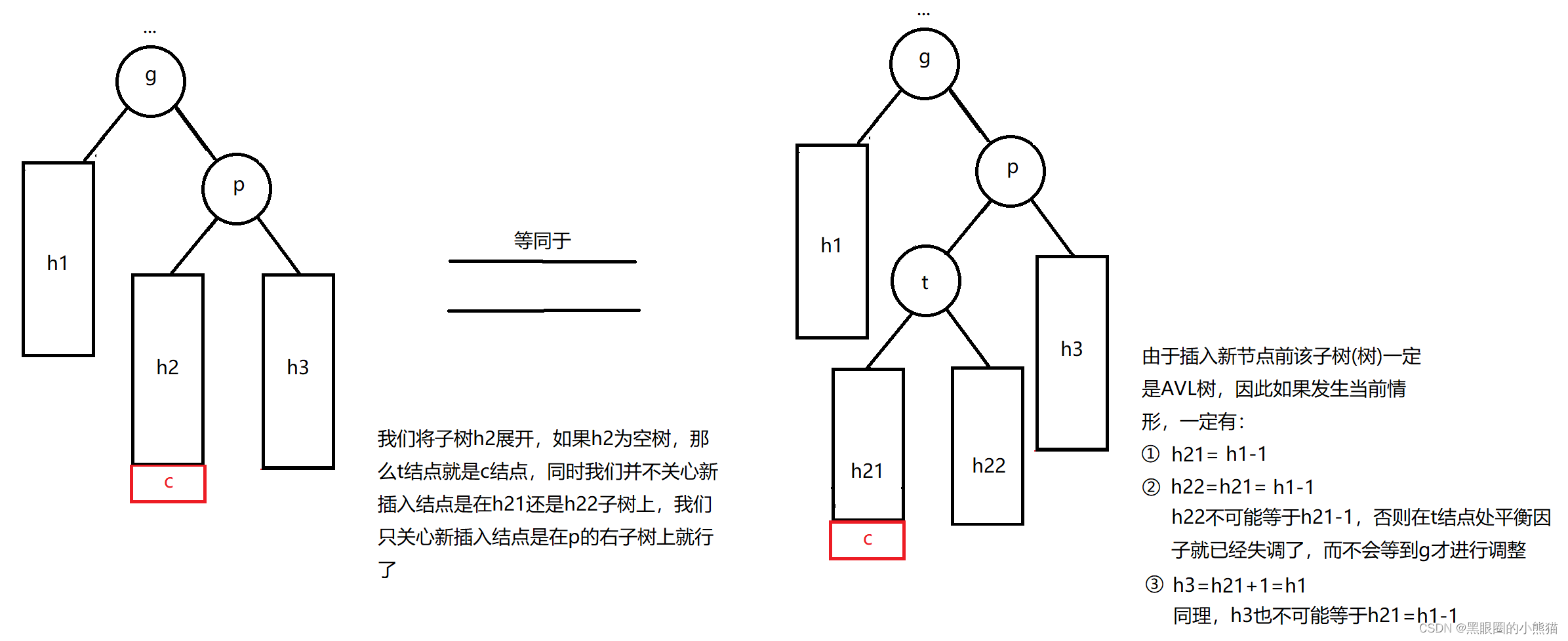
这种情况我们需要进行右左双旋，具体做法为：
1.以p结点为根结点进行右单旋
2.以g结点为根结点进行左单旋

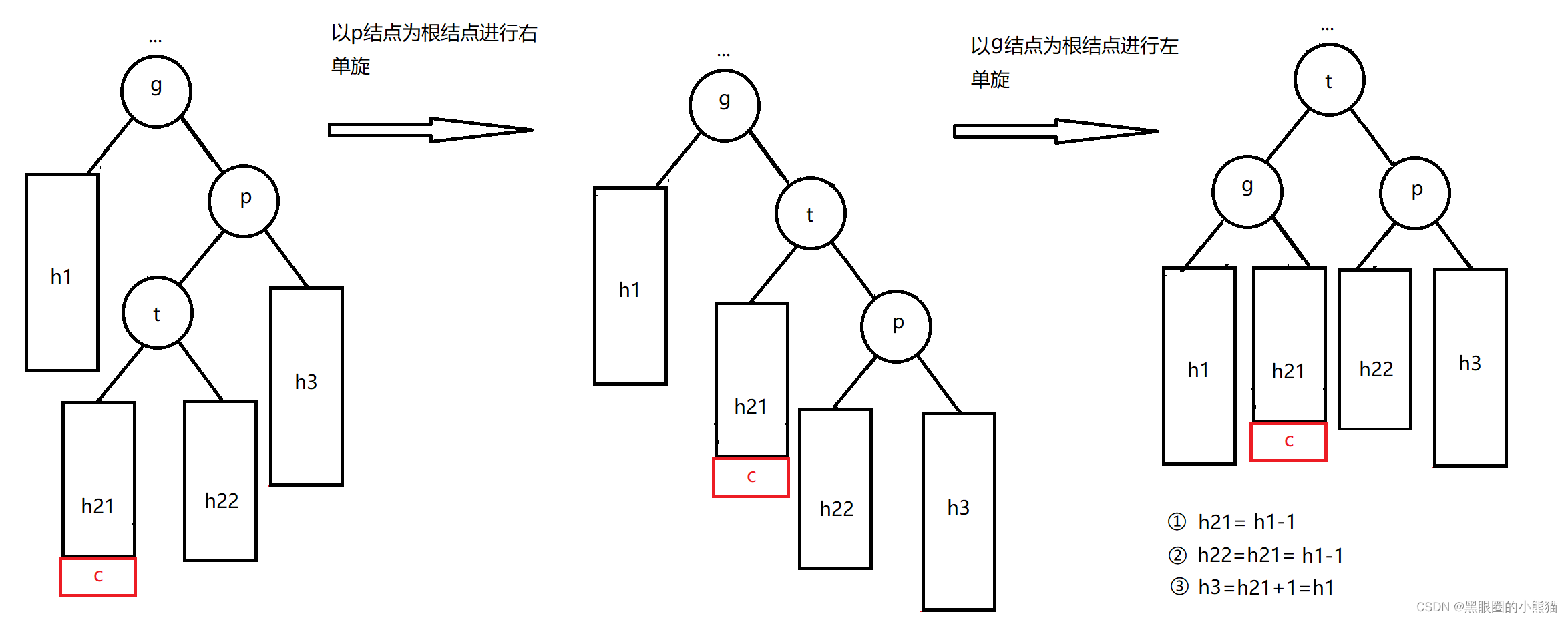
此时结点t的平衡因子也必定为0，调整后以p为根结点的子树的高度与插入结点前以g为根结点的子树高度相比并无变化，因此从p结点到根结点路径上面的祖先结点的平衡因子不需要再进行调整。

AVL树结点的删除我们不进行讨论，可以知道其结点的删除最坏情况下需要进行树的高度次的旋转，因此AVL树适用于数据是静态的情况，如果结构需要经常修改，AVL树就不太适用了。

代码实现

template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data = T()): _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _left;AVLTreeNode<T>* _right;AVLTreeNode<T>* _parent;T _data;int _bf;   // 节点的平衡因子
};template<class T>
class AVLTree
{typedef AVLTreeNode<T> Node;
public:AVLTree(): _root(nullptr){}// 在AVL树中插入值为data的节点bool Insert(const T& data){Node* cur = new Node(data);if (nullptr == _root){_root = cur;return true;}Node* tmp = _root;Node* parent = nullptr;//插入while (tmp){parent = tmp;if (cur->_data > tmp->_data){tmp = tmp->_right;}else if (cur->_data < tmp->_data){tmp = tmp->_left;}else{return false;}}if (cur->_data > parent->_data){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//调整平衡因子parent = cur;Node* grandpa = parent->_parent;while (grandpa){if (parent == grandpa->_left){--grandpa->_bf;}else{++grandpa->_bf;}if (2 == grandpa->_bf || -2 == grandpa->_bf)//旋转{if (parent == grandpa->_left && cur == parent->_left){//右单旋RotateR(grandpa);}else if (parent == grandpa->_right && cur == parent->_right){//左单旋RotateL(grandpa);}else if (parent == grandpa->_left && cur == parent->_right){//左右双旋RotateLR(grandpa);}else if (parent == grandpa->_right && cur == parent->_left){//右左双旋RotateRL(grandpa);}break;}else if (0 == grandpa->_bf){break;}cur = parent;parent = grandpa;grandpa = grandpa->_parent;}return true;}private:// 右单旋void RotateR(Node* parent){Node* left_child = parent->_left;parent->_left = left_child->_right;if (left_child->_right){left_child->_right->_parent = parent;}left_child->_right = parent;left_child->_parent = parent->_parent;if (parent->_parent){if (parent->_parent->_left == parent){//parent为其父结点的左孩子parent->_parent->_left = left_child;}else{//parent为其父结点的右孩子parent->_parent->_right = left_child;}}parent->_parent = left_child;if (_root == parent){_root = left_child;}//调整平衡因子left_child->_bf = 0;parent->_bf = 0;}// 左单旋void RotateL(Node* parent){Node* right_child = parent->_right;parent->_right = right_child->_left;if (right_child->_left){right_child->_left->_parent = parent;}right_child->_left = parent;right_child->_parent = parent->_parent;if (parent->_parent){if (parent->_parent->_left == parent){//parent为其父结点的左孩子parent->_parent->_left = right_child;}else{//parent为其父结点的右孩子parent->_parent->_right = right_child;}}parent->_parent = right_child;if (_root == parent){_root = right_child;}//调整平衡因子right_child->_bf = 0;parent->_bf = 0;}// 左右双旋void RotateLR(Node* parent){int pLR_bf = parent->_left->_right->_bf;RotateL(parent->_left);RotateR(parent);//调整平衡因子if (1 == pLR_bf){parent->_bf = 0;parent->_parent->_bf = 0;parent->_parent->_left->_bf = -1;}else if (-1 == pLR_bf){parent->_bf = 1;parent->_parent->_bf = 0;parent->_parent->_left->_bf = 0;}else if (0 == pLR_bf){parent->_bf = 0;parent->_parent->_bf = 0;parent->_parent->_left->_bf = 0;}}// 右左双旋void RotateRL(Node* parent){int pLR_bf = parent->_right->_left->_bf;RotateR(parent->_right);RotateL(parent);//调整平衡因子if (1 == pLR_bf){parent->_bf = -1;parent->_parent->_bf = 0;parent->_parent->_right->_bf = 0;}else if (-1 == pLR_bf){parent->_bf = 0;parent->_parent->_bf = 0;parent->_parent->_right->_bf = 1;}else if (0 == pLR_bf){parent->_bf = 0;parent->_parent->_bf = 0;parent->_parent->_right->_bf = 0;}}private:Node* _root;
};

红黑树

理论

红黑树通过颜色来控制树的高度，可以保证树的最大高度不会超过最小高度的2倍，其结点的颜色由以下规则来约束：
1.每个结点不是红色就是黑色
2.空节点可以看做是黑色结点
3.根结点是黑色的
4.一条路径上不能存在连续的红色结点（即如果当前结点是红色结点，那么其父亲结点和左右孩子结点必定是黑色的）
5.从根结点到叶子结点的每条路径上的黑色结点个数相同

由以上规则可知，红黑树的最小高度路径是该路径上的所有结点都是黑色的，最大高度路径是该路径上黑色和红色结点交替出现，这样就可以保证树的最大高度不会超过最小高度的2倍。

因此，只要遵循以上规则，红黑树的高度就可以保证。

我们需要在每个结点中增加一个变量color记录当前结点的颜色，在进行插入时，新插入的结点的颜色是红色，如果新插入结点的父结点的颜色是黑色的，则红黑树不需要进行任何调整，否则就需要调整。用c表示当前结点，p表示c的父亲结点，g表示c的祖父结点，u表示c的叔叔结点，其需要进行调整情况可以粗分为以下2种（细分5种)：

1. u存在且为红色结点
   我们只需要将p结点和u结点改为黑色，g改为红色，那么就可保证以g为根结点的子树必定遵循以上规则，接着将g赋给c，然后继续往上更新调整，直至不再出现连续红色结点或到根结点为止，如果更新到了根结点，我们最后必须让根结点变为黑色。
   

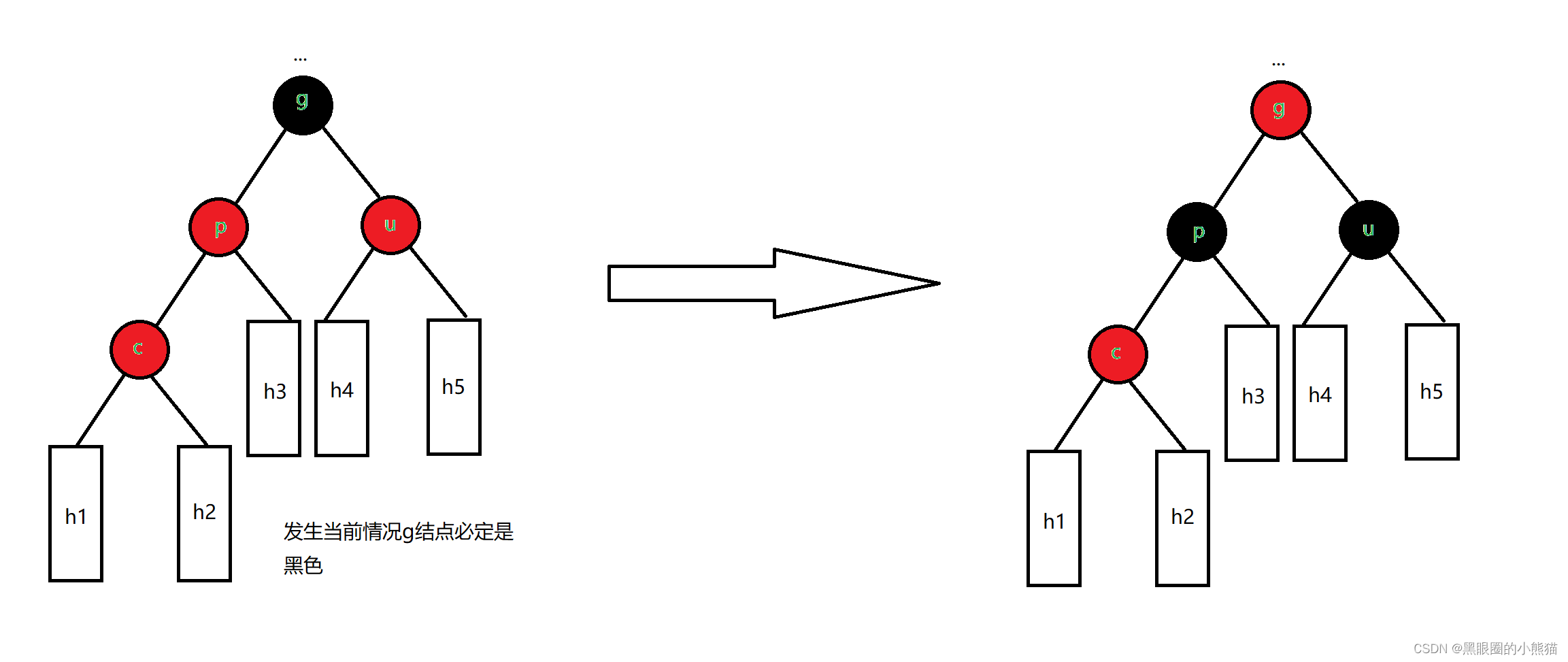
2. u为空结点或u为黑色结点
   ①c是p的左孩子，p是g左孩子
   我们只需要以g为根结点进行一次右单旋，然后将p结点改成黑色，g结点改成红色，就一定可以保证整棵树依旧是红黑树，不必再往上调整。
   

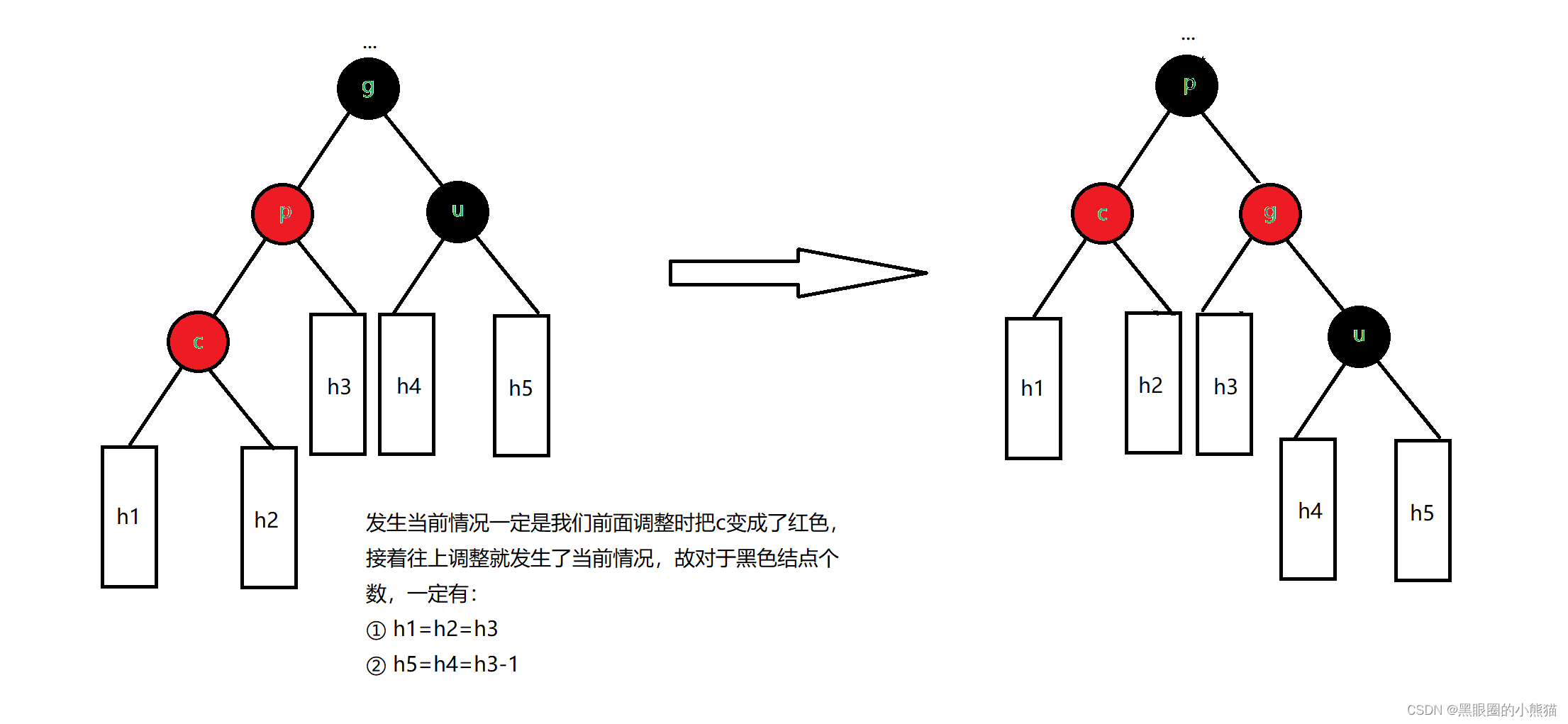
   ②c是p的右孩子，p是g右孩子
   我们只需要以g为根结点进行一次左单旋，然后将p结点改成黑色，g结点改成红色，就一定可以保证整棵树依旧是红黑树，不必再往上调整。
   

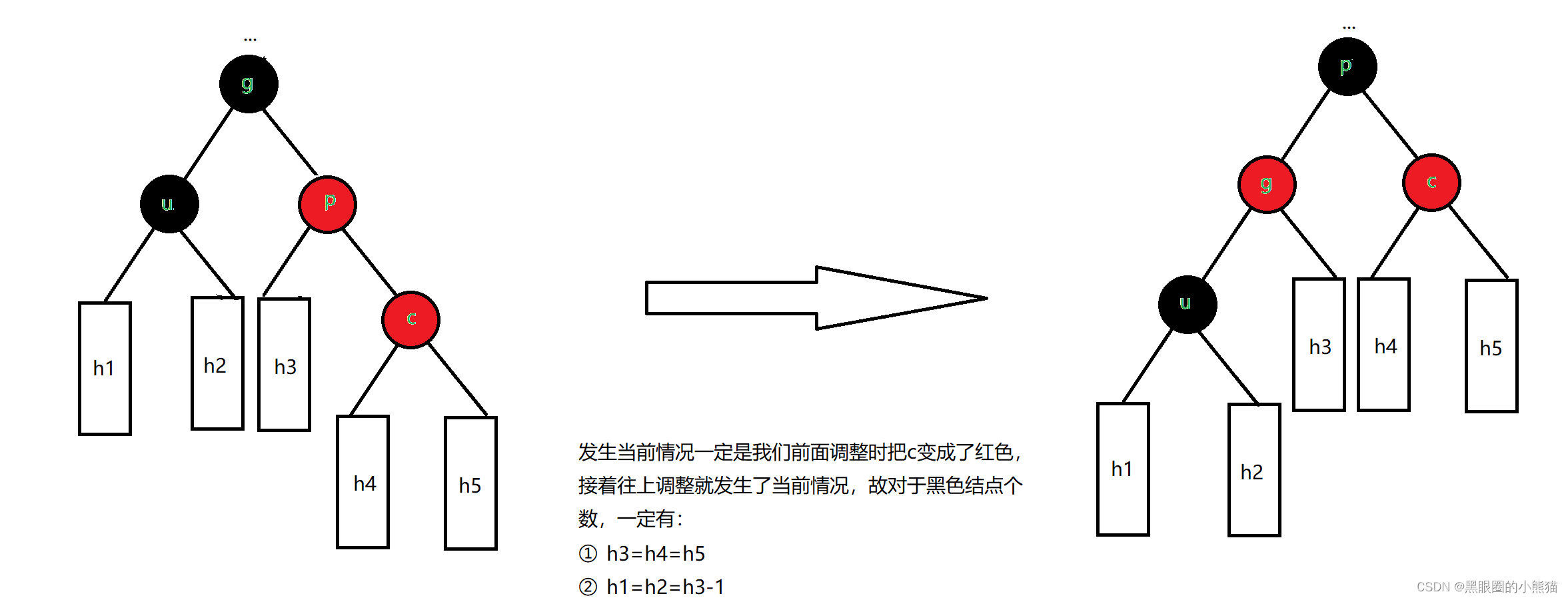
   ③c是p的右孩子，p是g左孩子
   我们只需要以p为根结点进行一次左单旋，然后以g为根结点进行一次右单旋，再将c结点改成黑色，g结点改成红色，就一定可以保证整棵树依旧是红黑树，不必再往上调整。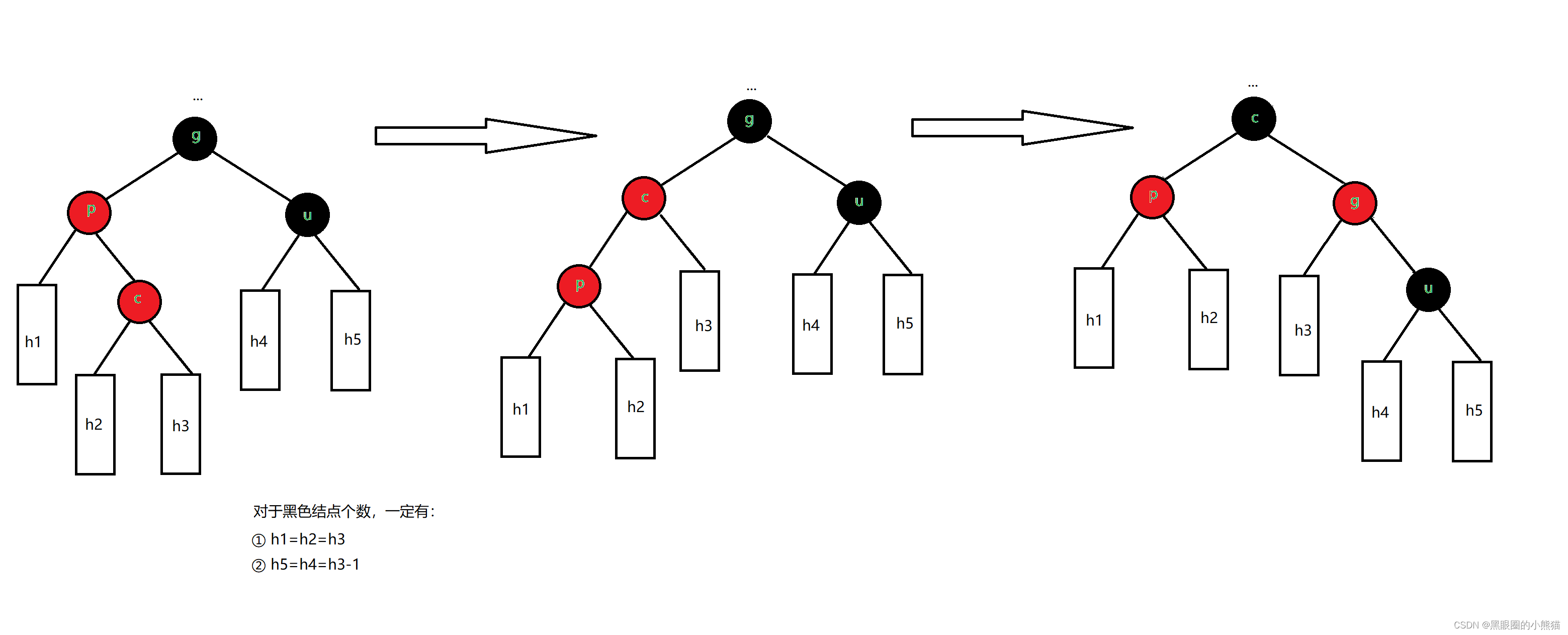

   ④c是p的左孩子，p是g右孩子
   我们只需要以p为根结点进行一次右单旋，然后以g为根结点进行一次左单旋，再将c结点改成黑色，g结点改成红色，就一定可以保证整棵树依旧是红黑树，不必再往上调整。
   
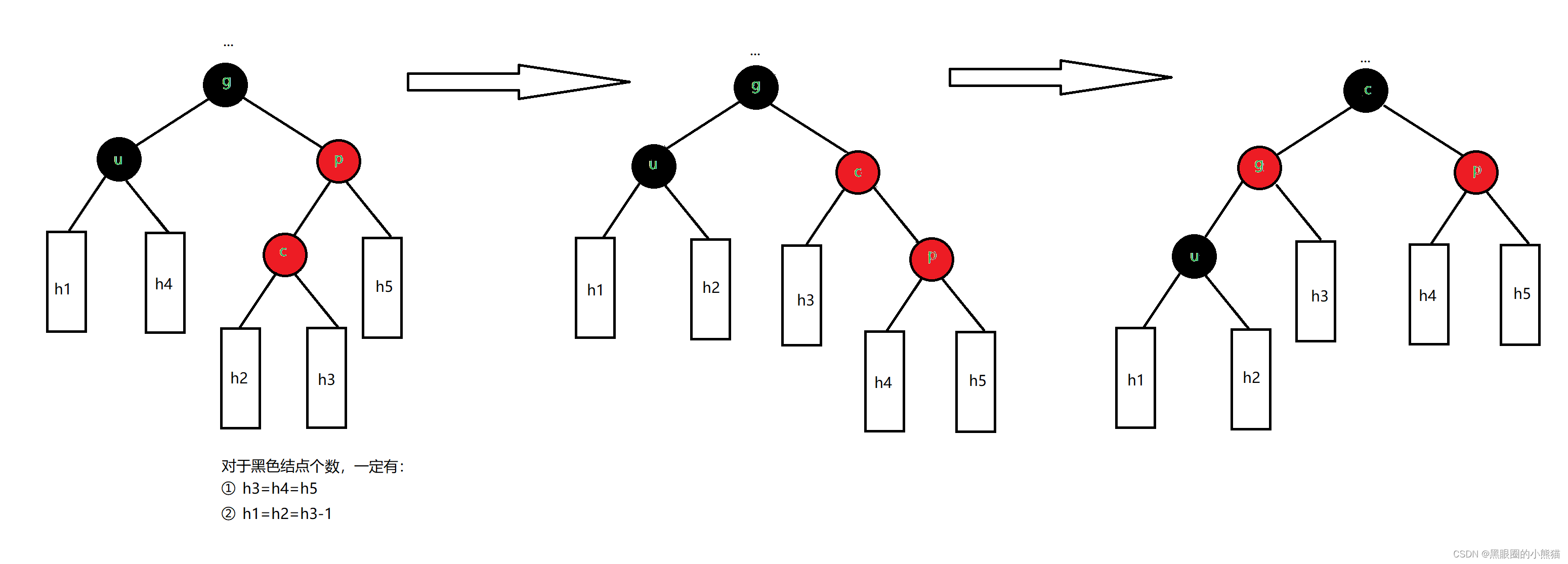
   红黑树结点的删除这里也不进行讨论。尽管红黑树的高度比AVL树高，但其在查找过程中性能与AVL树在同一个数量级上，为log(n)，且相比较于AVL树，红黑树降低了插入删除时旋转的次数，因此在经常增删的结构中红黑树的性能更优一点。

代码实现

enum Color
{red,black
};template<class T>
struct RBTreeNode
{RBTreeNode(const T& data = T()): _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _color(red){}RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Color _color;  // 节点颜色
};template<class T>
class RBTree
{typedef RBTreeNode<T> Node;
public:RBTree():_root(nullptr){}// 注意：为了简单起见，实现的红黑树不存储重复性元素bool Insert(const T& data){//节点插入Node* newNode = new  Node(data);if (_root == nullptr){_root = newNode;return true;}Node* cur = _root;while (cur){if (data > cur->_data && cur->_right){cur = cur->_right;}else if (data < cur->_data && cur->_left){cur = cur->_left;}else if (data == cur->_data){return false;}else{break;}}if (data > cur->_data){cur->_right = newNode;}else{cur->_left = newNode;}newNode->_parent = cur;//节点调整Node* grandpa =cur->_parent;Node* parent = cur;cur = newNode;while (nullptr!=grandpa){if (black == parent->_color){//cur节点的父节点为黑色，无需调整return true;}Node* uncle = grandpa->_right;if (parent == uncle){uncle = grandpa->_left;}if (uncle && red == uncle->_color){//叔叔节点存在且为红色uncle->_color = black;parent->_color = black;grandpa->_color = red;cur = grandpa;if (cur == _root){//如若cur已经是根节点，要将其修改为黑色cur->_color = black;break;}}else{//叔叔节点不存在或者叔叔节点为黑色if (parent == grandpa->_left && cur == parent->_left){//右单旋RotateR(grandpa);}else if (parent == grandpa->_right && cur == parent->_right){//左单旋RotateL(grandpa);}else if (parent == grandpa->_left && cur == parent->_right){//左右双旋RotateLR(grandpa);}else if (parent == grandpa->_right && cur == parent->_left){//右左双旋RotateRL(grandpa);}else{cout << "节点插入出错" << endl;exit(-1);}break;}parent = cur->_parent;grandpa = parent->_parent;}}private:// 左单旋void RotateL(Node* grandpa){//调整节点颜色grandpa->_color = red;grandpa->_right->_color = black;//节点旋转Node* right_child = grandpa->_right;grandpa->_right = right_child->_left;if (right_child->_left){right_child->_left->_parent = grandpa;}right_child->_left = grandpa;right_child->_parent = grandpa->_parent;if (grandpa->_parent){if (grandpa->_parent->_left == grandpa){//parent为其父结点的左孩子grandpa->_parent->_left = right_child;}else{//parent为其父结点的右孩子grandpa->_parent->_right = right_child;}}grandpa->_parent = right_child;if (_root == grandpa){_root = right_child;}}// 右单旋void RotateR(Node* grandpa){//调整节点颜色grandpa->_color = red;grandpa->_left->_color = black;//旋转节点Node* left_child = grandpa->_left;grandpa->_left = left_child->_right;if (left_child->_right){left_child->_right->_parent = grandpa;}left_child->_right = grandpa;left_child->_parent = grandpa->_parent;if (grandpa->_parent){if (grandpa->_parent->_left == grandpa){//grandpa为其父结点的左孩子grandpa->_parent->_left = left_child;}else{//grandpa为其父结点的右孩子grandpa->_parent->_right = left_child;}}grandpa->_parent = left_child;if (_root == grandpa){_root = left_child;}}//左右双旋void RotateLR(Node* grandpa){//调整节点颜色grandpa->_color = red;grandpa->_left->_right->_color = black;//旋转RotateL(grandpa->_left);RotateR(grandpa);}//右左双旋void RotateRL(Node* grandpa){//调整节点颜色grandpa->_color = red;grandpa->_right->_left->_color = black;//旋转RotateR(grandpa->_right);RotateL(grandpa);}private:Node* _root;
};