网站需要续费吗武汉网站竞价推广

第四节 空间直线及其方程

一、空间直线的一般方程

空间中的直线可以视为两个平面的交集。考虑两个相交平面Ⅱ₁和Ⅱ₂，它们的方程分别为 𝐴1𝑥+𝐵1𝑦+𝐶1𝑧+𝐷1=0A1​x+B1​y+C1​z+D1​=0 和 𝐴2𝑥+𝐵2𝑦+𝐶2𝑧+𝐷2=0A2​x+B2​y+C2​z+D2​=0。这两个平面的交线上的任一点必须同时满足这两个平面的方程。因此，直线可以通过方程组

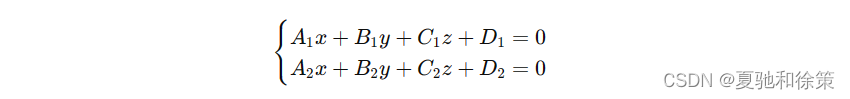
来表示，这称为直线的一般方程。

这种表示方法的优点在于其普遍性——任何两个相交平面都可以通过此方程组确定一条直线。但这也意味着直线的表达不是唯一的，因为存在无限多对相交平面可以定义同一条直线。

二、空间直线的对称式方程与参数方程

空间直线还可以通过对称式方程或点向式方程来表达。设直线上一点 𝑀0(𝑥0,𝑦0,𝑧0)M0​(x0​,y0​,z0​) 和一个方向向量 𝑠=(𝑚,𝑛,𝑝)s=(m,n,p) 已知，任意直线上的点 𝑀(𝑥,𝑦,𝑧)M(x,y,z) 与 𝑀0M0​ 之间的向量 𝑀0𝑀→=(𝑥−𝑥0,𝑦−𝑦0,𝑧−𝑧0)M0​M​=(x−x0​,y−y0​,z−z0​) 必须与方向向量 𝑠s 平行。因此，有：

这就是直线的对称式方程。

从对称式方程可以容易地导出参数方程：

其中 𝑡t 是参数。

例子：对称式方程及参数方程表示直线

给定直线方程 2𝑥−𝑦+3𝑧+4=02x−y+3z+4=0，首先确定直线上的一点。选择 𝑥0=1x0​=1，代入方程解得 𝑦0=0y0​=0 和 𝑧0=−2z0​=−2。再确定直线的方向向量，假设为 𝑠=(𝑚,𝑛,𝑝)s=(m,n,p)。这里我们可以找到两个平面的法线向量 𝑛1=(1,1,1)n1​=(1,1,1) 和 𝑛2=(2,−1,3)n2​=(2,−1,3)，它们的交线就是我们的直线，直线方向向量可以通过 𝑛1n1​ 和 𝑛2n2​ 的叉乘获得。

最终，直线的对称式方程和参数方程可由上述步骤得出，为：

对称式方程：𝑥−1𝑚=𝑦𝑛=𝑧+2𝑝对称式方程：

参数方程：𝑥=1+𝑚𝑡, 𝑦=𝑛𝑡, 𝑧=−2+𝑝𝑡参数方程：

这些方程不仅简洁地表达了空间直线的数学属性，还有助于直观地理解直线在三维空间中的位置和方向。

三、两直线的夹角

两条直线的夹角是指这两条直线的方向向量之间的角度，通常考虑的是它们的锐角或直角。设直线 𝐿1L1​ 和 𝐿2L2​ 的方向向量分别为 𝑠1=(𝑚1,𝑛1,𝑝1)s1​=(m1​,n1​,p1​) 和 𝑠2=(𝑚2,𝑛2,𝑝2)s2​=(m2​,n2​,p2​)，则这两条直线之间的夹角 𝜙ϕ 可以通过它们的方向向量的点积来确定：

这个公式反映了两向量间夹角的余弦值。如果结果为零，说明两直线互相垂直；如果余弦值的绝对值为 1，说明两直线平行或重合。

例2：求直线的夹角

设直线 𝐿1L1​ 的方向向量为 𝑠1=(1,−4,1)s1​=(1,−4,1)，直线 𝐿2L2​ 的方向向量为 𝑠2=(2,−2,−1)s2​=(2,−2,−1)。根据以上公式，我们可以计算两直线之间的夹角 𝜙ϕ。

首先计算点积和各向量的模：

因此：

从此我们可以得出两直线的夹角 𝜙ϕ。

四、直线与平面的夹角

直线与平面的夹角是指直线和它在该平面上的投影之间的夹角。如果直线与平面垂直，该夹角定义为 90 度。

设直线的方向向量为 𝑠=(𝑚,𝑛,𝑝)s=(m,n,p)，平面的法线向量为 𝑛=(𝐴,𝐵,𝐶)n=(A,B,C)。直线与平面的夹角 𝜃θ 可以通过它们的方向向量和法线向量的点积来确定：

这个公式反映了直线与平面的夹角的正弦值，适用于计算直线与平面非垂直的情况。如果 𝐴𝑚+𝐵𝑛+𝐶𝑝=0Am+Bn+Cp=0，则直线与平面平行或在平面上。

例3：求过点 (1, -2, 4) 且与平面 2𝑥−3𝑦+𝑧−4=02x−3y+z−4=0 垂直的直线的方程

因为所求直线垂直于已知平面，我们可以取该平面的法线向量 𝑛=(2,−3,1)n=(2,−3,1) 作为直线的方向向量。通过点和方向向量，直线的方程可以表示为：

这样，我们就得到了直线的方程，它通过给定的点并与给定平面垂直。

五、杂例

例4：求与两平面 𝑥−4𝑧=3x−4z=3 和 2𝑥−𝑦−5𝑧=12x−y−5z=1 的交线平行且过点 (−3,2,5)(−3,2,5) 的直线的方程

解法一

因为所求直线与两个平面的交线平行，直线的方向向量 𝑠s 必须同时与两个平面的法线向量 𝑛1=(1,0,−4)n1​=(1,0,−4) 和 𝑛2=(2,−1,−5)n2​=(2,−1,−5) 垂直。我们可以通过计算这两个法线向量的叉乘来找到直线的方向向量：

因此，直线的方程，使用点向式方程表示为：

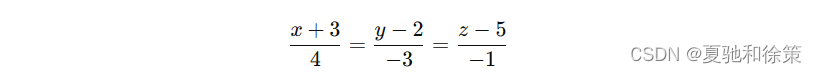
解法二

求过点 (−3,2,5)(−3,2,5) 且分别与两个平面平行的平面方程。第一个平面与 𝑥−4𝑧=3x−4z=3 平行，其方程为 𝑥−4𝑧=𝑘1x−4z=k1​，通过代入点 (−3,2,5)(−3,2,5) 得 𝑘1=−23k1​=−23。类似地，第二个平面与 2𝑥−𝑦−5𝑧=12x−y−5z=1 平行，其方程为 2𝑥−𝑦−5𝑧=𝑘22x−y−5z=k2​，通过代入点 (−3,2,5)(−3,2,5) 得 𝑘2=−33k2​=−33。

所求直线为这两个平面的交线，方程为：

例5：求直线与平面 2𝑥+𝑦+𝑧−6=02x+y+z−6=0 的交点

已知直线的参数方程为 𝑥=2+𝑡x=2+t, 𝑦=3+𝑡y=3+t, 𝑧=4+2𝑡z=4+2t。将这些参数方程代入平面方程：

解得 𝑡=−1t=−1。将 𝑡=−1t=−1 代入直线的参数方程，得交点的坐标为 (1,2,2)(1,2,2)。

例6：求过点 (2,1,3)(2,1,3) 且与直线垂直相交的直线的方程

先构造一个过点 (2,1,3)(2,1,3) 且垂直于已知直线的平面方程，该平面方程为：

3(𝑥−2)+2(𝑦−1)−(𝑧−3)=03(x−2)+2(y−1)−(z−3)=0

求已知直线与这个平面的交点，假设已知直线的参数方程为 𝑥=−1+3𝑡x=−1+3t, 𝑦=1+2𝑡y=1+2t, 𝑧=−𝑡z=−t。代入平面方程并求解得 𝑡t 的值，找到交点。

以点 (2,1,3)(2,1,3) 为起点，交点为终点的向量 是所求直线的一个方向向量，所以直线的方程为：

这些示例体现了空间解析几何在解决与平面和直线相关的问题中的强大应用。