网站建设安全协议关键词歌曲

1. 定义

数学优化问题是：在给定约束条件下，找到一个目标函数的最优解（最大值或最小值）。

2. 快速get理解

初学者对优化技术陌生的话，可以把 “求解优化问题” 理解为 “解一个不等式方程组”，解方程的。

以下我们用几个简单的例子来讲述什么是优化问题。
引用说明：下面的公式来自MindOpt新发布的基于大模型的AI工程师生成的内容截图，或者案例广场的案例里面的截图。

a. 比如一个鸡兔同笼问题：

有一笼兔子和鸡，兔子和鸡各有一个头，兔子有4只脚，鸡有两只脚。笼子上有 35 个头，下有94 个脚。请问兔子和鸡的数目各是多少？

对应的数学公式如下：

可以看到公式是两个 “等号 = ” 描写的约束关系的方程组。
这个时候算出来的结果是：

• 兔子的数量x=12
• 鸡的数量y=23

b. 而一个优化问题。 会增加不等式关系，然后增加了一个目标。比如上面的例子更改下：

有一笼兔子和鸡，兔子和鸡各有一个头，兔子有4只脚，鸡有两只脚。笼子上有头至少有30个，下面脚至多80个。要想兔子最多，请问最多有多少个兔子？

这个时候，对应的数学公式的约束就是个不等式的关系；另外，增加了个maximize x，也就是优化的目标。

这个时候，如果只考虑不等式的约束，解可能就是个域（有多种解、多个可行域）。
比如 x=1,y=29; x=3,y=29; x=3, y= 30……等等

增加了要将x最大化这个目标，就相当于在这个域里面找最大值。这个时候可以利用优化求解器进行计算，得出最优目标时候的变量取值，如下

• 兔子的数量 x=10,
• 鸡的数量y=20.

需要注意的是，在有些情况下，最优目标时的变量取值也有可能是个域（多解）的情况。

这里，是不是有高中学线性规划的感觉了？比如下面的高一题目，是不是很熟悉？

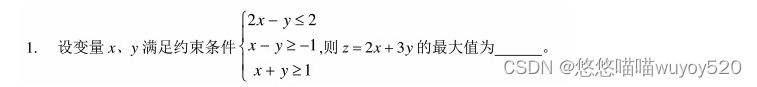
3. 拓展思路

3.1 拓展应用场景

在业务场景中使用优化的方法来描述业务遇到的问题。比如：

电商平台要为一家新兴手游公司进行广告推广，平台有两种广告类型可供选择：类型A、类型B、类型C。广告类型A的转化率为5%，每投放一次费用为10元；广告类型B的转化率为8%，每投放一次费用为15元; 广告类型B的转化率为7.7%，每投放一次费用为12元。手游公司需要至少获得1000次投放，并且总费用不能超过20000元。每种类型广告都希望至少投放5次。平台希望最大化累计转化数，要如何规划广告投放？

得到如下的优化问题数学公式：

最后用优化求解器算得的解是：

广告类型A投放次数=5
广告类型B投放次数=6
广告类型C投放次数=1655
目标函数值 = 128.165

3.2 拓展问题维度和类型

上面的问题都只有几个变量（未知数），还比较简单，如果有很多的变量呢，方程将很长，一般是用矩阵的方式来表达。比如：

也有用 大sigma 来表达求和∑的，比如下面几个金融投资里面应用的优化问题：

这里还关注下几个数学概念：

• x * x，代表二次。优化问题里面常说的“线性”就是一次关系，y =3x就是一次的，线性关系。y = 4 x*x 就是二次的，属于非线性关系。

• 如果有的变量只能是整数，不能是小数，就是“离散的”。与之相对的是“连续的”。离散的问题优化起来会方法不一样，会变困难，因此经常有问题需要松弛下，使得变为连续的。

• 还有问题 “凸” 和 “非凸”。凸优化是个研究生课程，比较难。普通人需要掌握凸问题更好求解，非凸不好求解，因此列数学公式描述业务问题时，尽量避免非凸的情况。

4. 更丰富的优化问题类型列表

更进一步的，优化问题的数学模型根据不同的业务有很复杂的模型。基本就是要掌握好：可以控制的变量、不等式关系的约束、优化目标的情况。

不同的数学模型适合不同的场景，在优化问题计算的时候，也会有不同的复杂度。

常见的问题类型会以下的词汇来描述：

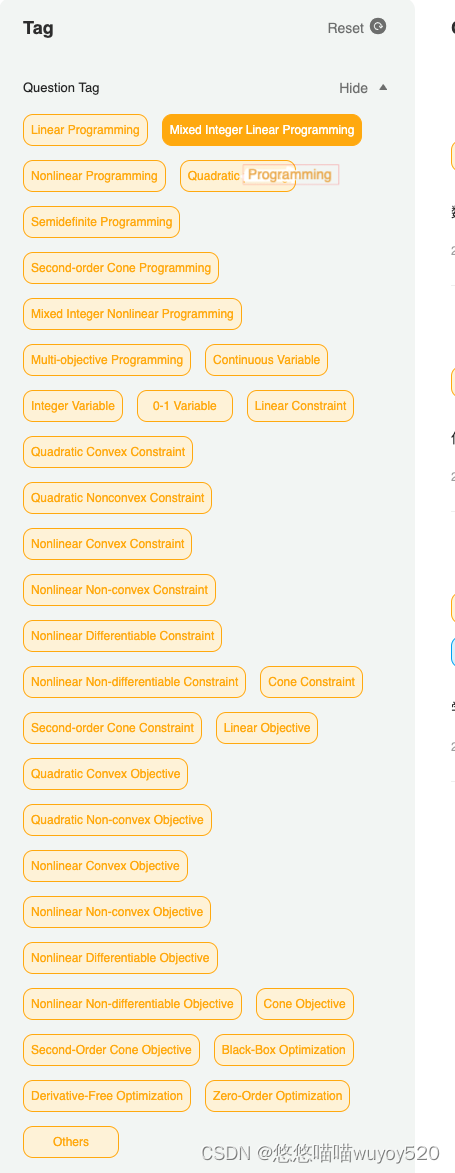比如

• 线性规划，英文是Linear Programming，简称LP，对应的数说目标函数是线性关系。
• 如果加上变量有些是整数（integer），则组合成MILP（Mixed Integer Programming），混合整数的线性规划问题。
• 如果目标里面有二次项，则称为二次规划 QP（Quadratic Programming）。
• 如果约束里面有二次项，则称为二次约束规划 QC （Quadratic Constraint），组合还有QCQP
• 再进一步的根据目标约束的类型，还可以进一步分类描述不同类型的问题
• 再进一步，根据问题的优化计算方式，还可以取名字，比如零阶优化、黑盒优化等

类目很多，可遇到了后再查询标准术语。

4. 优化问题的应用

优化问题在运筹学、工程、经济学、物流、能源、金融等许多领域有应用。属于底层的数学技术， 应用面很广。在航空、航天、国防等也有应用。

对应的求解优化问题的优化求解器可以广泛应用于电力系统调度、生产计划、物流路径规划、投资组合优化等多个领域。使用优化求解器可以帮助用户更方便、更快速地找到问题的最优解。

推荐可以去阿里达摩院求解器的案例广场看看，了解应用场景，和对应的简单的数学模型、源代码。

5. 优化问题的计算

在实际业务里，一般情况下不太需要关心求解的方法，是借助工具来完成计算。更多地是需要了解不同算法计算的复杂度，是否能快速求解，如果不能，如何变更优化问题，使得能快速求解。

在选择或者研究求解器时，一般会评估如下特性：

• 是否能求解
• 求解速度
• 稳定性
• 大规模问题求解能力和计算资源占用
• 接口易用性

小编这里推荐去MindOpt的平台去看商用的和开源的求解器软件，从这个案例，复制项目进去用：https://opt.aliyun.com/example/vqaeimyI3iEj 。全程浏览器里面操作，不需要操心软件安装和License。

更多的优化软件，可以参考我之前的博客：https://blog.csdn.net/wuyoy520/article/details/134185148