四川建设网站中国局势最新消息今天
优先级队列----堆
- 优先级队列
- 堆
- 堆的创建
- 堆的插入:
- 堆的删除:
- PriorityQueue的特性
- PriorityQueue的构造与方法
优先级队列
优先级队列: 不同于先进先出的普通队列,在一些情况下,优先级高的元素要先出队列。而这种队列需要提供两个基本的操作:返回最高优先级对象 和 添加新的对象。
(JDK1.8中,优先级队列底层使用的是 堆 数据结构,而堆则是在完全二叉树的基础上进行了调整)
堆
堆: 将一组集合的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 为 小堆,Ki >= K2i+1 且 Ki >= K2i+2 为 大堆。i = 0,1,2…,将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。例如:
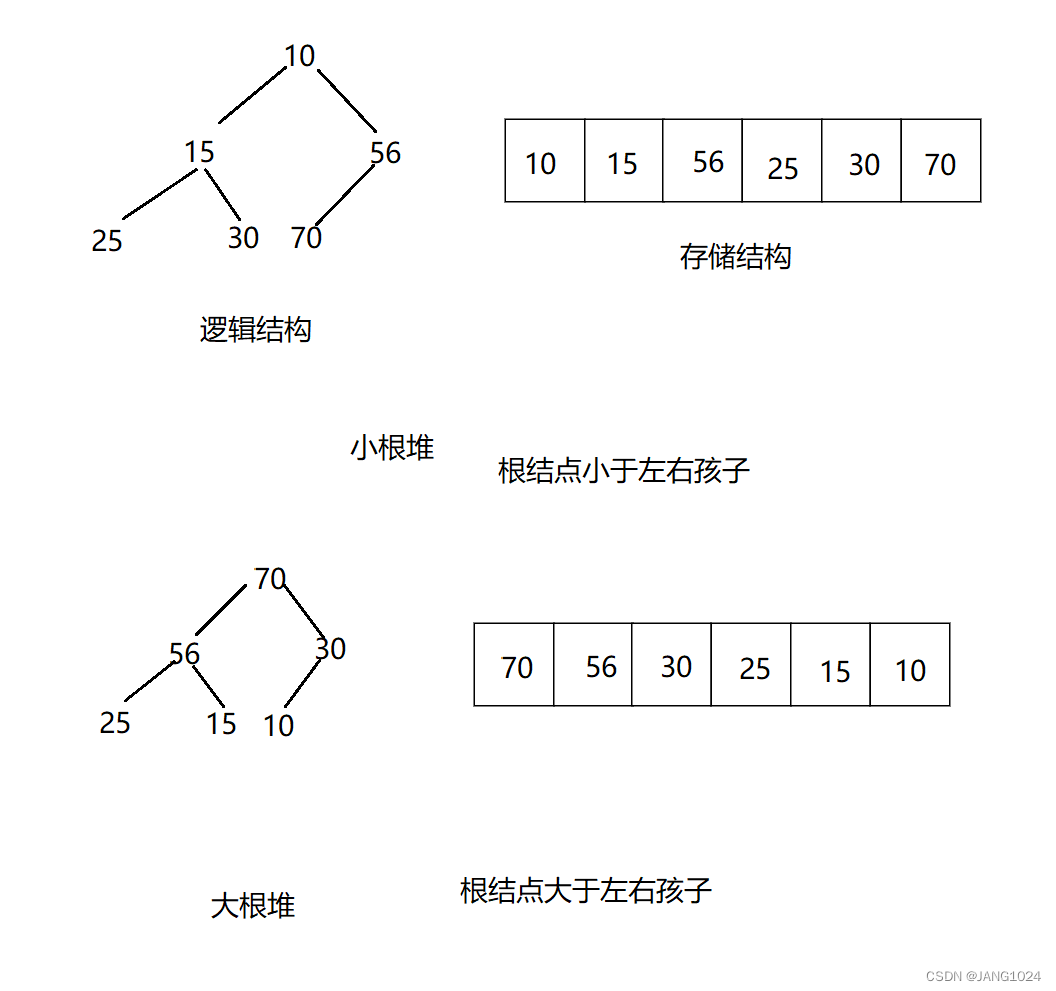
堆的两个性质:
堆中某个结点的值总是不大于或不小于其父节点的值。
堆总是一棵完全二叉树。
堆的存储方式:
堆是一棵完全二叉树,因此可以用层序的规则采用顺序的方式来高效存储,但对于非完全二叉树,就不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节
点,就会导致空间利用率比较低。
如果 i 表示孩子结点,则父节点为 (i - 1)/2。
如果 i 表示根结点,左孩子则为 2i + 1,右孩子为 2i + 2。
堆的创建
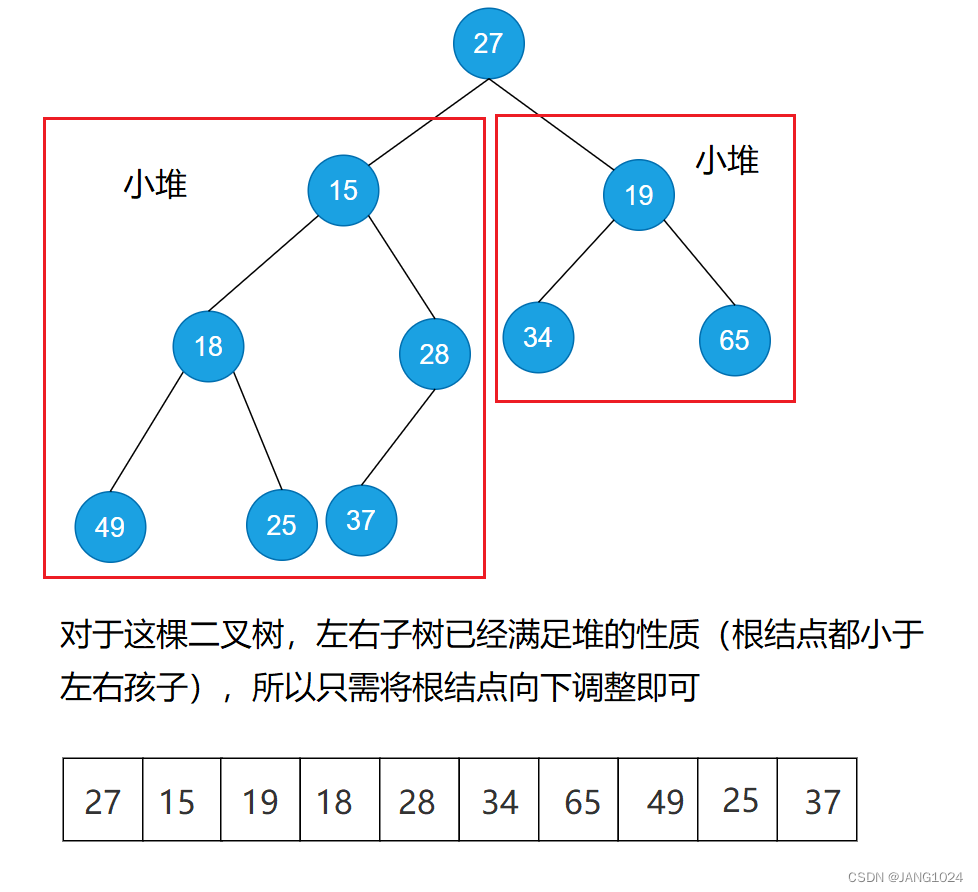
向下调整过程(以小根堆为例):
- 让 parent 标记需要调整的节点,child 标记 parent 的左孩子(完全二叉树中,一定先有左孩子)
- 如果 parent 的左孩子存在(child < size),进行以下操作,直到 parent 的左孩子不存在:
找到左右孩子中较小的结点,和 parent 进行比较,若 parent 小,则调整结束。若 parent 大,则进行交换。交换后,可能会使原来满足堆的子树发生改变,所以需要继续向下调整。
例如:
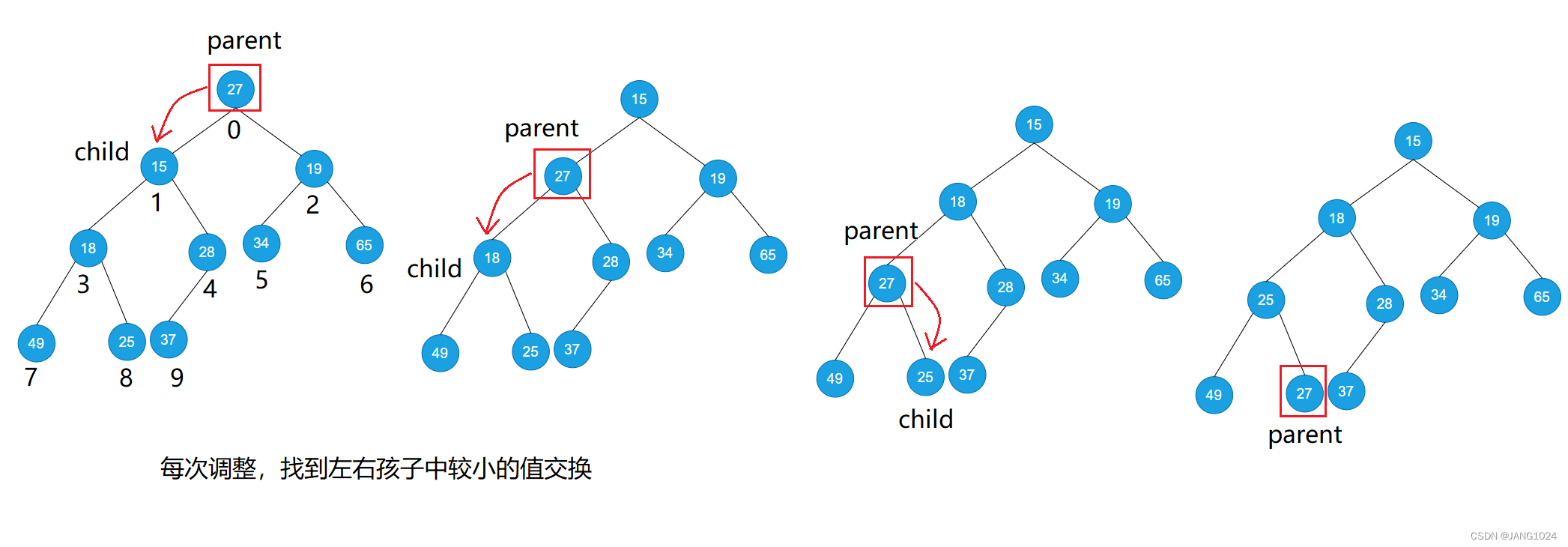
代码:
public class TestHeap {public int[] elem;public int usedSize;public TestHeap() {this.elem = new int[10];}//初始化public void initElem(int[] array) {for (int i = 0; i < array.length; i++) {elem[i] = array[i];usedSize++;}}public void createHeap() {//循环调用for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(parent, usedSize);}}//向下调整 len为当前有效数据个数private void shiftDown(int parent, int len) {int child = 2 * parent + 1;//最起码 要有左孩子while (child < len) {//一定是有右孩子的情况下if (child + 1 < len && elem[child] > elem[child + 1]) {//保证 child指向较小值child++;}if (elem[child] < elem[parent]) {//孩子结点小于父节点 交换int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;//继续调整下面子树parent = child;child = 2 * parent + 1;} else {break;}}}
}
建堆的时间复杂度:

堆的插入:
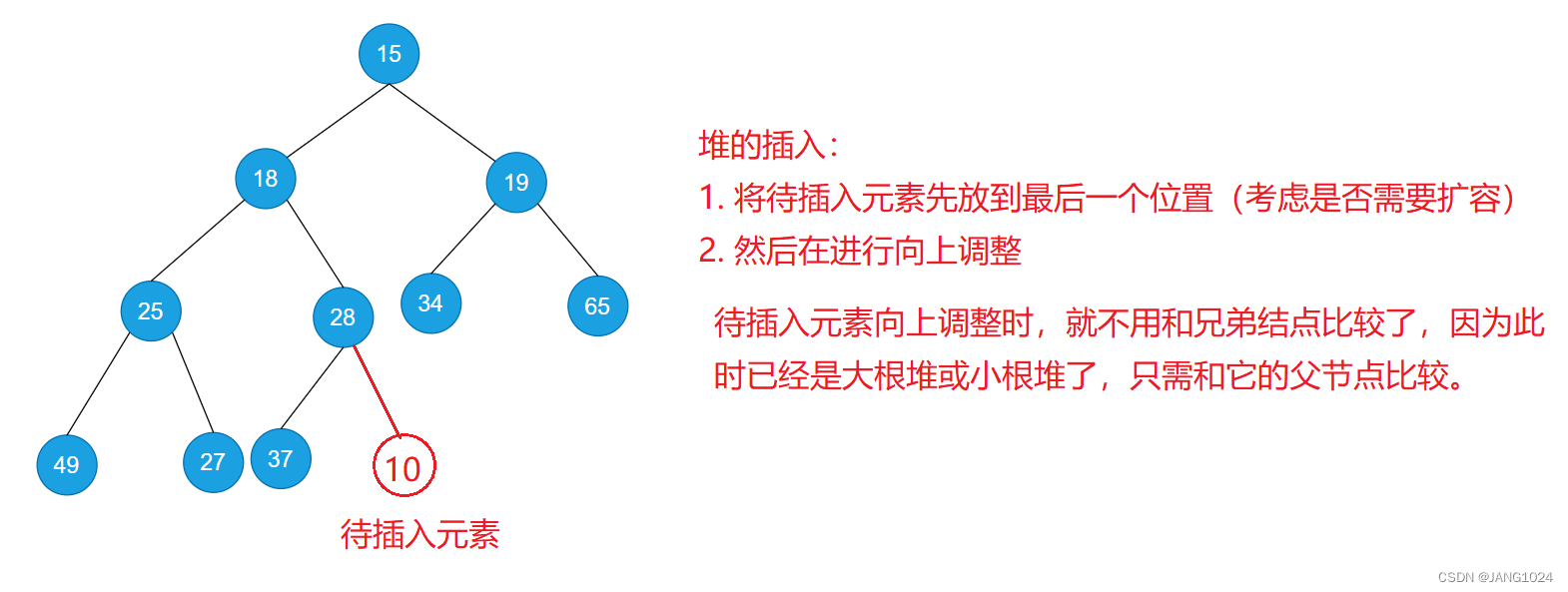
代码:
public void offer(int val) {if (isFull()) {//满了扩容elem = Arrays.copyOf(elem, 2 * elem.length);}//放到最后一个位置,长度加一elem[usedSize++] = val;//向上调整shiftUp(usedSize-1);}public boolean isFull() {return usedSize == elem.length;}private void shiftUp(int child) {int parent = (child - 1) / 2;while (child > 0) {if (elem[child] < elem[parent]) {int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;//继续往上走child = parent;parent = (child - 1) / 2;}else {break;}}}
堆的删除:
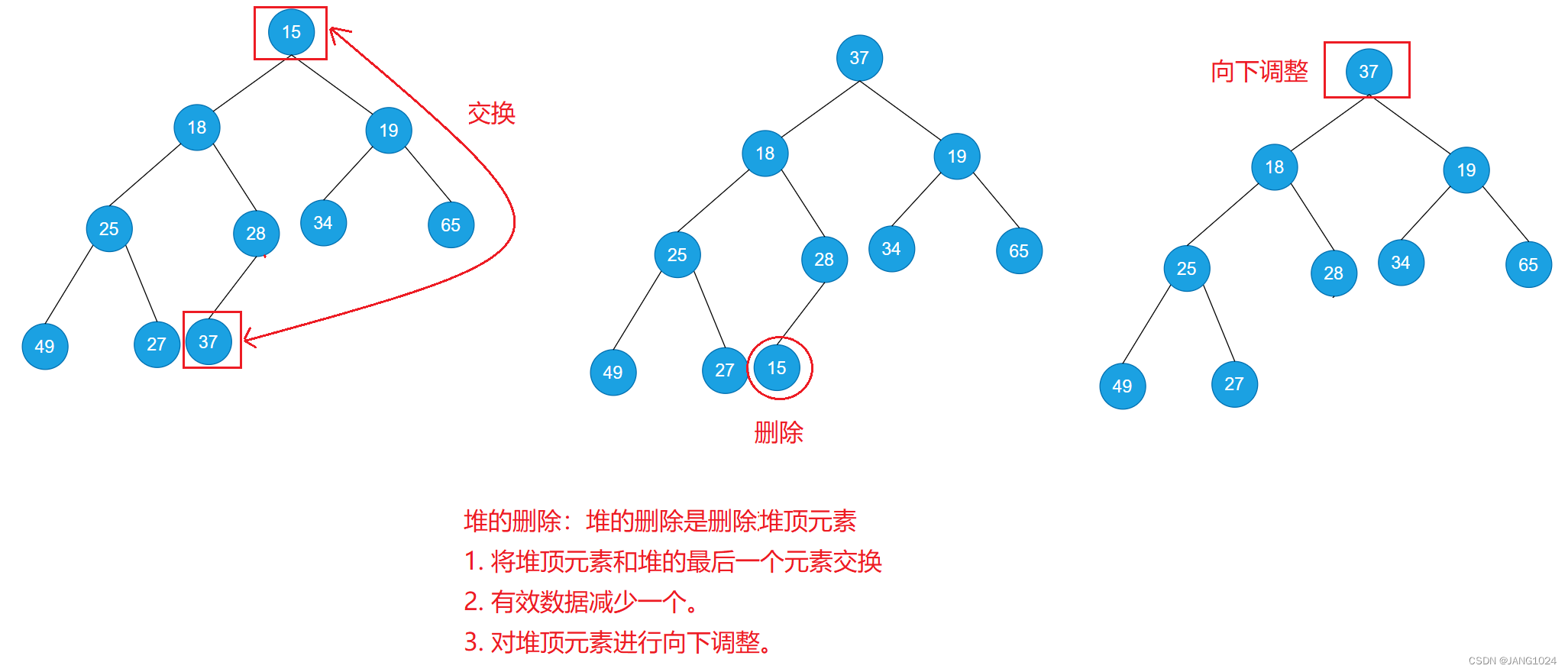
代码:
public void pop() {if (isEmpty()) {return;}//交换int tmp = elem[0];elem[0] = elem[usedSize - 1];elem[usedSize - 1] = tmp;//有效数据个数减一usedSize--;//向下调整shiftDown(0, usedSize);}public boolean isEmpty() {return usedSize == 0;}
PriorityQueue的特性
Java 集合框架中提供了 PriorityQueue 和 PriorityBlockingQueue 两种类型的优先级队列,PriorityQueue 是线程不安全的,PriorityBlockingQueue 是线程安全的,这里主要介绍PriorityQueue。
使用 PriorityQueue 需要注意:
-
使用时必须导入 PriorityQueue 所在的包(import java.util.PriorityQueue;)。
-
PriorityQueue 中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出 ClassCastException 异常。
只插入一个元素时,并不会报错:
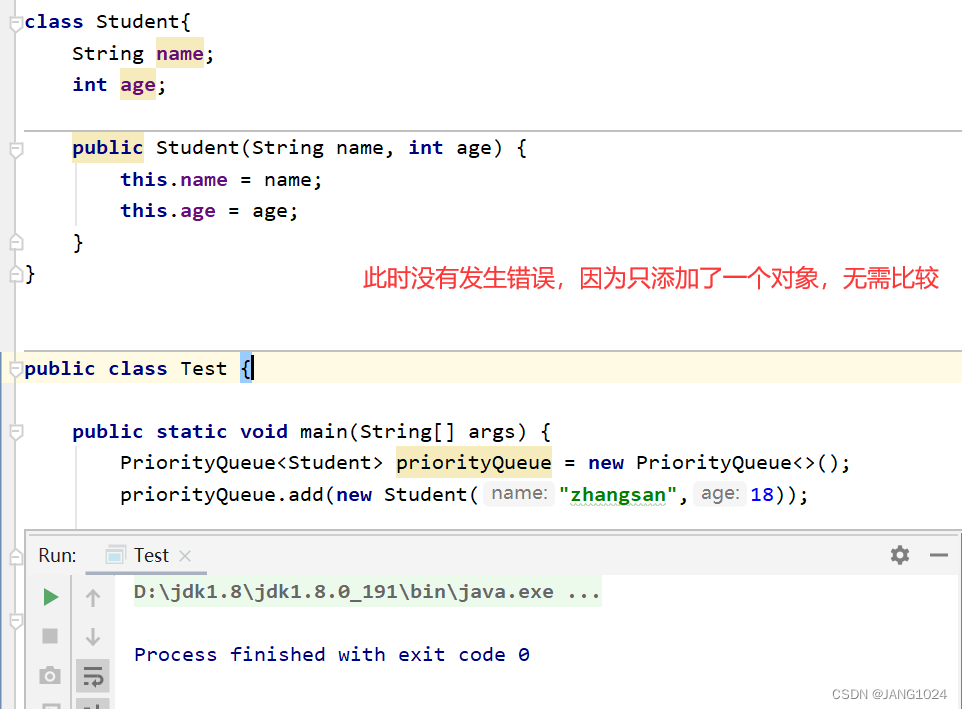
插入多个元素就会报错:
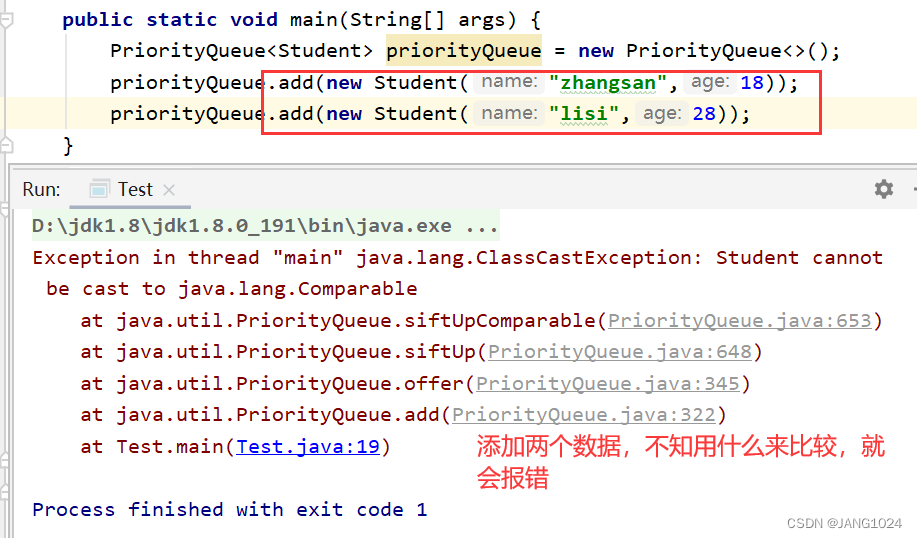
-
不能插入 null 对象,否则会抛出 NullPointerException。
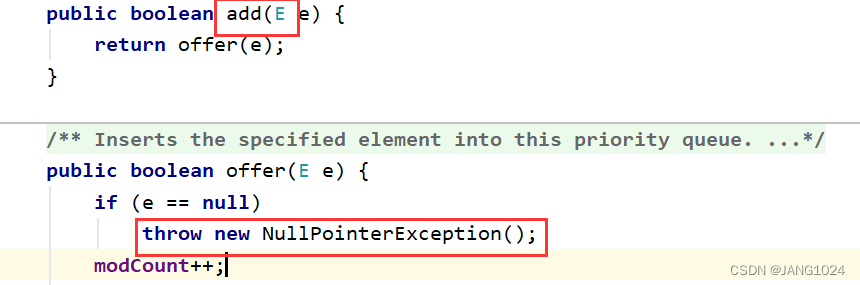
-
内部可以自动扩容。

-
插入和删除元素的时间复杂度为 O(log₂N)。
-
PriorityQueue 底层使用的是堆数据结构。
-
PriorityQueue 默认情况下是小堆。
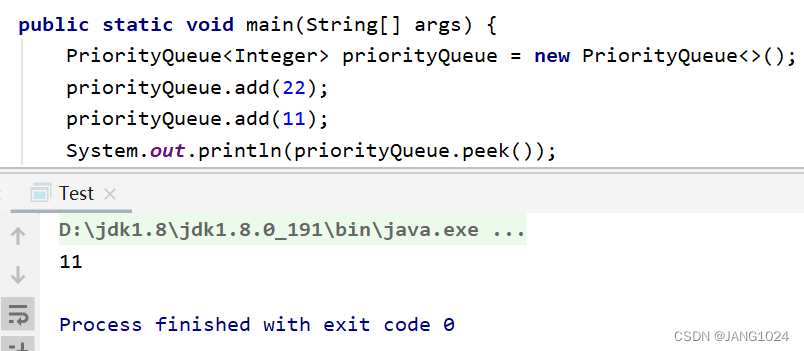
PriorityQueue的构造与方法
PriorityQueue 的几种构造方法:
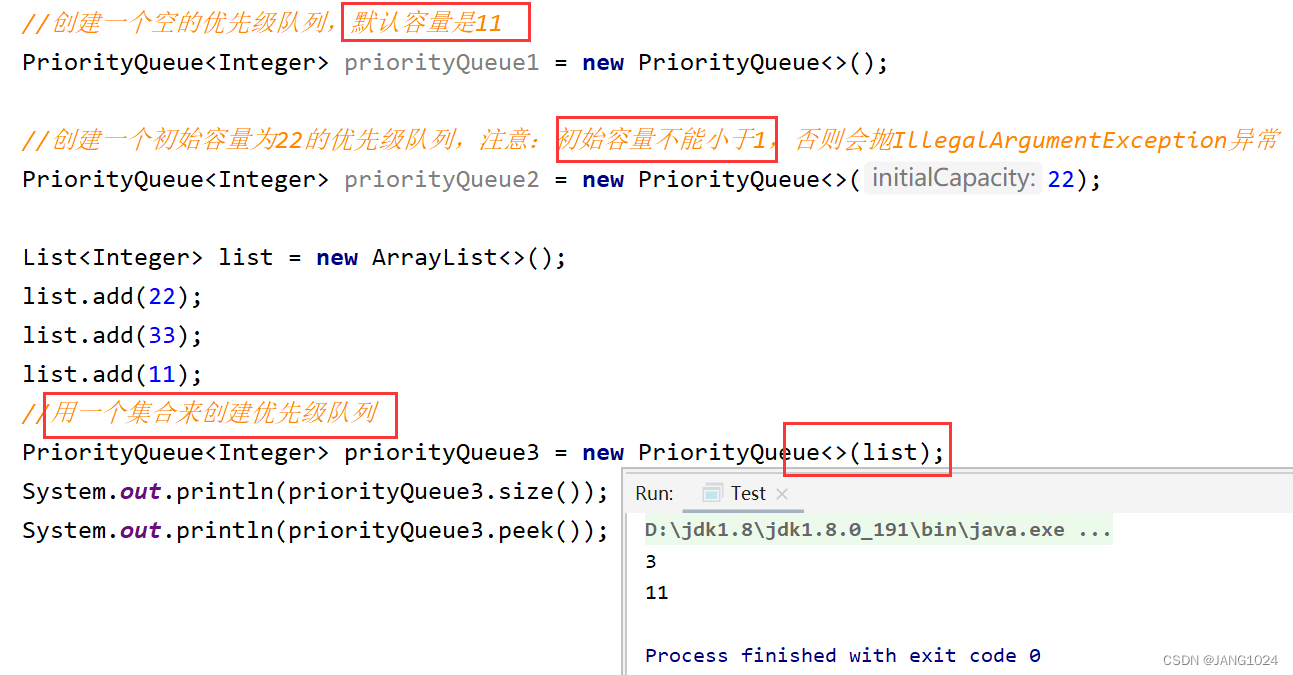
PriorityQueue 的方法:
PriorityQueue 的方法和其它数据结构类似:
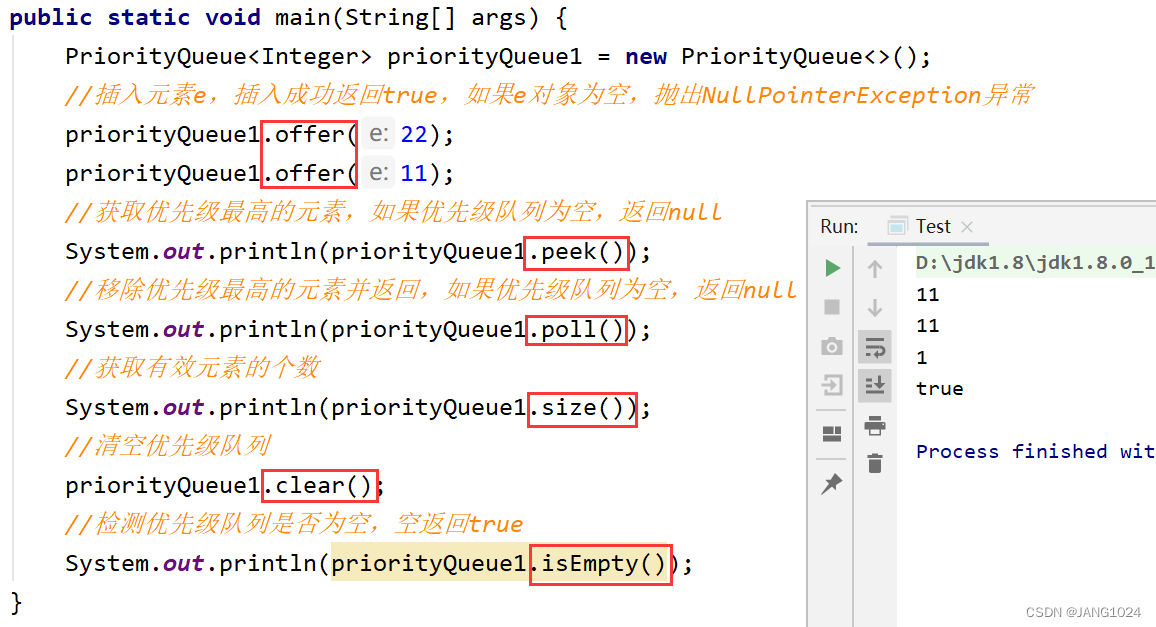
Top-k 问题: 最大或者最小的前k个数据。例如求一组数据中前 k 个最小的数据。
题目链接:leetcode----面试题 17.14. 最小K个数
题目描述:
思路一:我们可以初始化一个数组大小的堆,然后遍历数组的同时将元素放进堆中,默认是小根堆,所以取 k 次堆顶元素即可(删除堆顶元素后,会调整堆中的数据)。
代码:
public int[] smallestK(int[] arr, int k) {//存储最小K个数的数组int[] ret = new int[k];if (arr == null || k == 0) {return ret;}// 以数组长度初始化一个小根堆Queue<Integer> minHeap = new PriorityQueue<>(arr.length);//遍历数组 放进小根堆for (int value : arr) {minHeap.offer(value);}//取 k个堆顶元素for (int i = 0; i < k; i++) {ret[i] = minHeap.poll();}return ret;
}
上面这段代码会使时间复杂度升高,每添加或删除一个元素,就会调整一个接近数组长度的堆。
思路二:要求最小 k 个数,我们将数组里的前 k 个元素添加到一个大小为 k 的大根堆,因为是大根堆,所以堆顶元素是堆中最大的元素,然后遍历数组剩下的元素,如果数组剩下的元素比堆顶元素小,我们就删除堆顶元素,并添加数组的元素,如果数组剩下的元素比堆顶元素大,它就不会是前 k 个最小数。
代码:
public int[] smallestK(int[] arr, int k) {int[] ret = new int[k];if (arr == null || k == 0) {return ret;}//提供比较器,重写compare方法,此时建立的就是大根堆Queue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});//将数组前k个元素添加到大根堆中for (int i = 0; i < k; i++) {maxHeap.offer(arr[i]);}//遍历数组未添加到堆中的元素for (int i = k; i < arr.length; i++) {//因为是求最小值,所以如果比大根堆的堆顶元素小,就删除堆顶元素,并添加这个元素到堆中if (arr[i] < maxHeap.peek()) {maxHeap.poll();maxHeap.offer(arr[i]);}}//将堆中的k个元素添加中数组中for (int i = 0; i < k; i++) {ret[i] = maxHeap.poll();}return ret;
}
这段代码中,只建立了 k 个容量大小的堆,调整的个数就比第一段代码少。
对于求一组数据中前 k 个最大或最小的元素时,数据少时我们可以排序,但对于数据特别多时,还是采用堆的方式比较合适。步骤如下:
- 用数据集合中前K个元素来建堆。
求前 k 个最大的元素,则建小堆
求前 k 个最小的元素,则建大堆 - 用剩余的 N-K 个元素依次与堆顶元素来比较,不满足则替换堆顶元素,堆中剩余的 K 个元素就是所求的前 K 个最小或者最大的元素。
