高端广告公司网站建设东莞网络营销全网推广

1- 过拟合 欠拟合 模型选择

1-1 欠拟合：

• 在训练集和测试集上都不能很好的拟合数据【模型过于简单】
  原因： 学习到的数据特征过少

• 解决办法：
  1.得到更多的特征【特征组合，添加上下文特征，平台的特征】.
  2.添加多项式特征，使得模型的泛化能力更强.

1-2 过拟合：

• 在训练集上表现很好，在测试集上表现不好【模型过于复杂】

• 问题： 特征存在异常，噪声，模型过于复杂

• 过拟合的一些解决办法

  • 1.正则化：L1正则【使得特征系数为0 –Lasso回归】/L2正则【使得特征系数趋近于0–Ridge回归】
  • 2.在神经网络里面：设置drop out 随机失活
  • 3.提前终止训练 early stopping【正则化迭代学习方法，在验证错误率达到最小值的时候停止训练，通过限制错误率的阈值，进行停止】
  • 4.随机森林里面：预剪枝和后剪枝
  • 5.增加数据量【重采样】，清洗数据
  • 6.减少特征维度，防止维度灾难
  • 7.降低模型的复杂度，采用交叉验证等.

1-3 模型选择

• 模型选择是指如何选择最适合数据的模型。在选择模型时，需要考虑模型的复杂度、泛化能力、可解释性、训练时间和计算资源等因素。

常用的模型选择方法包括交叉验证、网格搜索、贝叶斯优化等。

• 交叉验证可以评估不同模型的性能
• 网格搜索可以在参数空间中搜索最优参数
• 贝叶斯优化则可以更有效地搜索参数空间
  
  

2- 正则L1与L2

为了防止过拟合，通常在线性的模型的基础上引入一个正则化项。$L_1$和$L_2$正则化中，正则项是模型参数的$L_1$范数和$L_2$范数。

• $L_1$: $\underset{w}{\min }{\sum }_{i=1}^m(y_i-w^T{x}_i{)}^2+\lambda ||w|{|}_1$，当λ>0,就是Lasso回归,λ=0就是线性回归
• $L_2$: $\underset{w}{\min }{\sum }_{i=1}^m(y_i-w^T{x}_i{)}^2+\lambda ||w|{|}_2^2$，当λ>0,就是岭回归，一般写成$\underset{w}{\min }{\sum }_{i=1}^m(y_i-w^T{x}_i{)}^2+\frac{\lambda }{2n}\sum w^2$

Lasso回归中的L1正则项是绝对值之和，使得某些特征系数为0，岭回归中的L2正则项是平方和，使得某些特征系数趋近于0

#弹性网络 Elastic Net 综合lasso和ridge两个方法
from sklearn.linear_model import Ridge, ElasticNet, Lasso

Lasso回归和岭回归都是基于最小二乘法（OLS）的基础上进行的。OLS是通过最小化实际值和预测值之间的误差平方和来得到模型参数的，但是它容易产生过拟合的问题。为了解决这个问题，Lasso回归和岭回归引入了正则化项，对模型参数进行限制。

Lasso回归（Least Absolute Shrinkage and Selection Operator Regression）

• 通过在目标函数中加入L1正则项，将模型参数向零稀疏化。L1正则化在优化过程中会将一些不重要的特征对应的参数收缩到零，从而实现了特征选择的功能。Lasso回归可以在高维数据中寻找到较少的重要特征，从而提高了模型的泛化能力。

岭回归（Ridge Regression）

• 通过在目标函数中加入L2正则项，将模型参数平滑化。L2正则化在优化过程中会让所有参数都往零收缩，但是不会将任何参数完全收缩到零，从而保留了所有的特征，避免了Lasso回归可能出现的特征丢失问题。岭回归在处理多重共线性问题时效果很好，可以有效减少共线性带来的影响。

总之，Lasso回归和岭回归都是非常有用的正则化方法，可以在机器学习任务中提高模型的性能和稳定性。当数据集具有大量特征、多重共线性或者存在噪声时，这两种方法都可以用来提高模型的泛化能力和减少过拟合的风险

3- L2正则代码复现

3-1 底层逻辑实现

创建一个高维线性回归实验
$y=0.05+{\sum }_{i=1}^{p}0.01x_i+\epsilon$，ε服从均值为0，标准差为0.01的正态分布
特征维度为200，将训练数据集的样本设低20

import numpy as np
import torch
import torch.nn as nn
#
n_train,n_test,num_inputs = 20,100,200#样本，特征
true_w,true_b = torch.ones(num_inputs,1)*0.01,0.05#生成特征
features =torch.randn((n_train+n_test,num_inputs))
labels = torch.matmul(features,true_w)+true_b
labels += torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float)
#划分训练集和测试及
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]

模型相关函数

#画图
def use_svg_display():# 用矢量图显示display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):use_svg_display()# 设置图的尺寸plt.rcParams['figure.figsize'] = figsize
def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,legend=None, figsize=(3.5, 2.5)):set_figsize(figsize)plt.xlabel(x_label)plt.ylabel(y_label)plt.semilogy(x_vals, y_vals)if x2_vals and y2_vals:plt.semilogy(x2_vals, y2_vals, linestyle=':')plt.legend(legend)

def init_params():w = torch.randn((num_inputs,1),requires_grad = True)b = torch.zeros(1,requires_grad=True)return [w,b]
#定义L2范数,惩罚项
def l2_penalty(w):return (w**2).sum()/2
#定义模型
def linreg(X, w, b): return torch.mm(X, w) + b
#定义代价
def squared_loss(y_hat, y):# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2return (y_hat - y.view(y_hat.size())) ** 2 / 2
#定义随机梯度下降
def sgd(params, lr, batch_size):  # for param in params:param.data -= lr * param.grad / batch_size#封装数据
dataset = torch.utils.data.TensorDataset(train_features,train_labels)
train_iter = torch.utils.data.DataLoader(dataset,batch_size,shuffle=True)

训练

batch_size,num_epochs,lr = 1,100,0.003#批次，迭代次数，学习率
#模型与损失均方误差函数
net=linreg
loss=squared_loss
#
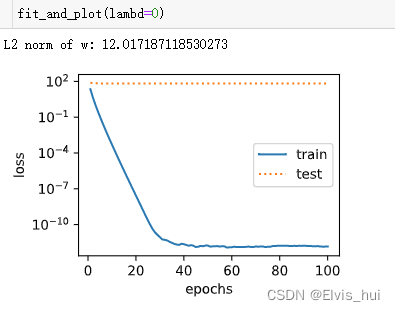
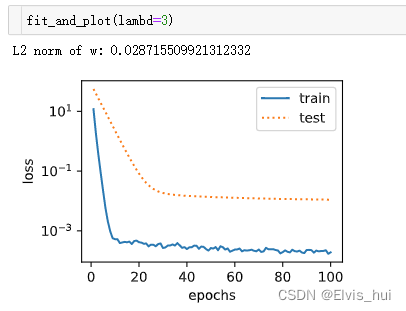
def fit_and_plot(lambd):w,b=init_params()train_ls,test_ls=[],[]for _ in range(num_epochs):for X,y in train_iter:l = loss(net(X,w,b),y)+lambd*l2_penalty(w)l = l.sum()if w.grad is not None:#梯度清0w.grad.data.zero_()n.grad.data.zero_()l.backward()#反向传播sgd([w,b],lr,batch_size)#参数更新train_ls.append(loss(net(train_features,w,b),train_labels).mean().item())test_ls.append(loss(net(test_features,w,b),test_labels).mean().item())semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',range(1, num_epochs + 1), test_ls, ['train', 'test'])print('weight:', net.weight.data,'\nbias:', net.bias.data)

观察过拟合λ=0的情况

使用L2,λ>0

3-2 简洁实现

num_inputs = 200
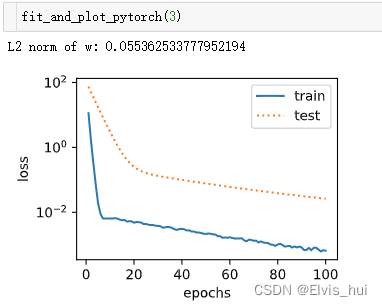
def fit_and_plot_pytorch(wd):#对权重参数衰减，权重名称一般是以weight结尾net = nn.Linear(num_inputs ,1)nn.init.normal_(net.weight,mean=0,std=1)nn.init.normal_(net.bias,mean=0,std=1)optimizer_w = torch.optim.SGD(params = [net.weight],lr=lr,weight_decay=wd)#weight_decay权重衰减optimizer_b = torch.optim.SGD(params=[net.bias],lr=lr)#不对偏置进行衰减train_ls,test_ls = [],[]for _ in range(num_epochs):for X,y in train_iter:l = loss(net(X),y).mean()optimizer_w.zero_grad()optimizer_b.zero_grad()l.backward()#更新权重参数optimizer_w.step()optimizer_b.step()train_ls.append(loss(net(train_features),train_labels).mean().item())test_ls.append(loss(net(test_features),test_labels).mean().item())semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',range(1, num_epochs + 1), test_ls, ['train', 'test'])print('L2 norm of w:', net.weight.data.norm().item())	

wd=0

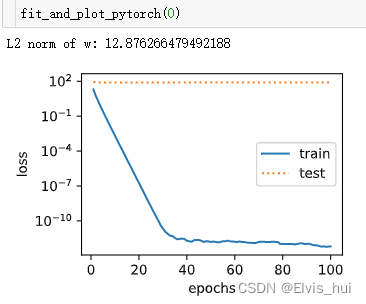
wd>0