网站运营维护工作内容线上宣传的方式

第一题

题目来源

64. 最小路径和 - 力扣（LeetCode）

题目内容

解决方法

方法一：动态规划

可以使用动态规划来解决这个问题。

1. 首先创建一个与网格大小相同的二维数组dp，用于存储从起点到每个位置的最小路径和。
2. 然后初始化dp[0][0] = grid[0][0]，表示起点的最小路径和为起点的值。
3. 接下来进行动态规划的遍历，遍历顺序可从起点开始按行或按列遍历。对于每个位置dp[i][j]，其最小路径和为grid[i][j]加上它左边或上边位置的最小路径和的较小值。

复杂度分析：

时间复杂度：

• 遍历网格中的每个元素，所以需要进行两层嵌套循环，总共遍历次数为m * n，其中m为网格的行数，n为网格的列数。
• 在每次循环中，执行常数时间的操作，将上方和左方的最小路径和与当前位置的值相加，然后取最小值。
• 因此，整体的时间复杂度为O(m * n)。

空间复杂度：

• 创建了一个与网格大小相同的二维数组dp，用于存储从起点到每个位置的最小路径和。因此需要额外的空间来存储这些最小路径和。
• dp数组的大小为m * n，与原始网格的大小相同。
• 所以，空间复杂度为O(m * n)。

综上所述，该算法的时间复杂度为O(m * n)，空间复杂度为O(m * n)。

LeetCode运行结果：

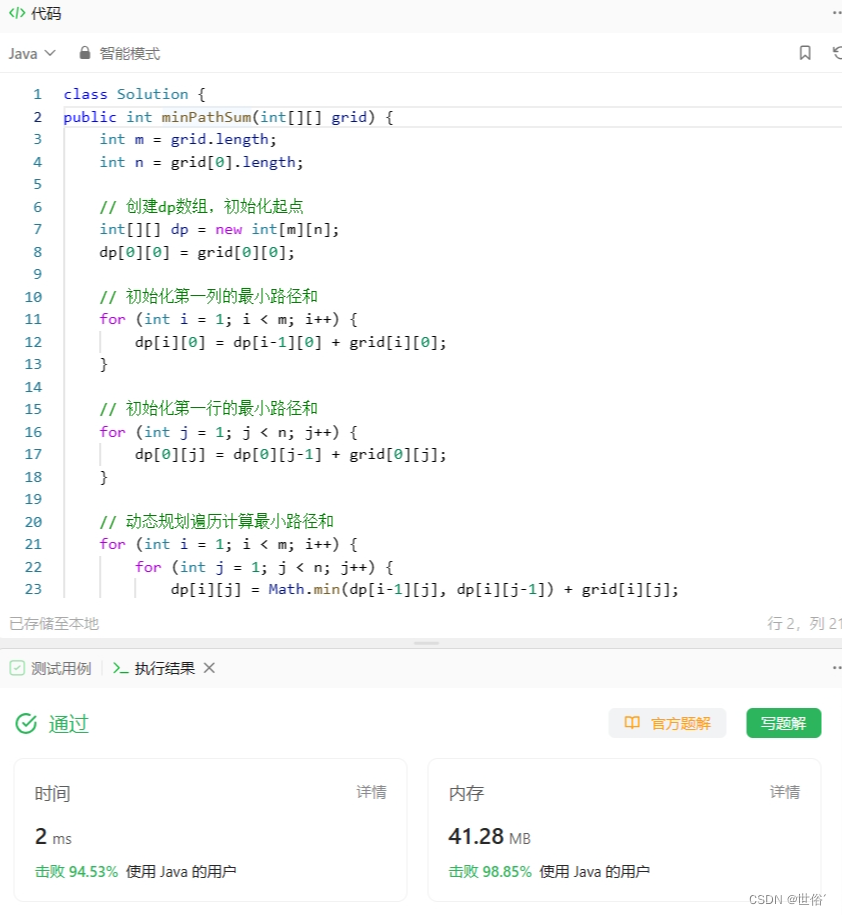
第二题

题目来源

65. 有效数字 - 力扣（LeetCode）

题目内容

解决方法

方法一：有限状态自动机

可以使用有限状态自动机（DFA）来解决该问题。我们需要设计合适的状态集合以及状态转移规则。其中，状态包括以下几种：

起始空格状态：在这个状态下，前面的空格已经被忽略。 符号位状态：在这个状态下，可能出现 + 或 -。 整数状态：在这个状态下，输入了数字 0-9。 小数点状态：在这个状态下，已经输入了小数点。 小数状态：在这个状态下，已经输入了数字并带有小数点。 幂符号状态：在这个状态下，出现了字符 e 或 E。 幂符号后的符号位状态：在这个状态下，出现了符号位 + 或 -。 幂符号后的整数状态：在这个状态下，输入了数字 0-9。 终止状态：如果当前输入的字符不合法或者最后一步能够到达终止状态，则说明输入是一个合法的数字。

class Solution {
public boolean isNumber(String s) {// 定义有限状态自动机Map<State, Map<CharType, State>> transfer = new HashMap<>(); transfer.put(State.STATE_INITIAL, new HashMap<>() {{put(CharType.CHAR_SPACE, State.STATE_INITIAL); // 起始空格状态put(CharType.CHAR_NUMBER, State.STATE_INTEGER); // 整数状态put(CharType.CHAR_SIGN, State.STATE_SIGN); // 符号位状态put(CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT); // 小数点状态（前面没有数字）}});transfer.put(State.STATE_SIGN, new HashMap<>() {{put(CharType.CHAR_NUMBER, State.STATE_INTEGER); // 整数状态put(CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT); // 小数点状态（前面没有数字）}});transfer.put(State.STATE_INTEGER, new HashMap<>() {{put(CharType.CHAR_NUMBER, State.STATE_INTEGER); // 整数状态put(CharType.CHAR_EXP, State.STATE_EXP); // 幂符号状态put(CharType.CHAR_POINT, State.STATE_POINT); // 小数状态put(CharType.CHAR_SPACE, State.STATE_END); // 终止状态}});transfer.put(State.STATE_POINT, new HashMap<>() {{put(CharType.CHAR_NUMBER, State.STATE_FRACTION); // 小数状态put(CharType.CHAR_EXP, State.STATE_EXP); // 幂符号状态put(CharType.CHAR_SPACE, State.STATE_END); // 终止状态}});transfer.put(State.STATE_POINT_WITHOUT_INT, new HashMap<>() {{put(CharType.CHAR_NUMBER, State.STATE_FRACTION); // 小数状态}});transfer.put(State.STATE_FRACTION, new HashMap<>() {{put(CharType.CHAR_NUMBER, State.STATE_FRACTION); // 小数状态put(CharType.CHAR_EXP, State.STATE_EXP); // 幂符号状态put(CharType.CHAR_SPACE, State.STATE_END); // 终止状态}});transfer.put(State.STATE_EXP, new HashMap<>() {{put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER); // 幂符号后的整数状态put(CharType.CHAR_SIGN, State.STATE_EXP_SIGN); // 幂符号后的符号位状态}});transfer.put(State.STATE_EXP_SIGN, new HashMap<>() {{put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER); // 幂符号后的整数状态}});transfer.put(State.STATE_EXP_NUMBER, new HashMap<>() {{put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER); // 幂符号后的整数状态put(CharType.CHAR_SPACE, State.STATE_END); // 终止状态}});transfer.put(State.STATE_END, new HashMap<>() {{put(CharType.CHAR_SPACE, State.STATE_END); // 终止状态}});// 根据定义的状态转移规则，判断该字符串是否为有效数字int length = s.length();State state = State.STATE_INITIAL;for (int i = 0; i < length; i++) {CharType type = toCharType(s.charAt(i));if (!transfer.get(state).containsKey(type)) { // 当前输入不合法return false;}state = transfer.get(state).get(type); // 进入下一个状态}// 最后一步能够到达终止状态说明该字符串是一个有效数字return state == State.STATE_INTEGER || state == State.STATE_POINT ||state == State.STATE_FRACTION || state == State.STATE_EXP_NUMBER ||state == State.STATE_END;
}// 定义字符类型枚举类
enum CharType {CHAR_NUMBER,CHAR_EXP,CHAR_POINT,CHAR_SIGN,CHAR_SPACE,CHAR_ILLEGAL
}// 判断字符类型
private CharType toCharType(char ch) {if (ch >= '0' && ch <= '9') {return CharType.CHAR_NUMBER;} else if (ch == 'e' || ch == 'E') {return CharType.CHAR_EXP;} else if (ch == '.') {return CharType.CHAR_POINT;} else if (ch == '+' || ch == '-') {return CharType.CHAR_SIGN;} else if (ch == ' ') {return CharType.CHAR_SPACE;} else {return CharType.CHAR_ILLEGAL;}
}// 定义状态枚举类
enum State {STATE_INITIAL,STATE_INTEGER,STATE_POINT,STATE_POINT_WITHOUT_INT,STATE_FRACTION,STATE_EXP,STATE_EXP_SIGN,STATE_EXP_NUMBER,STATE_SIGN,STATE_END
}
}

复杂度分析：

• 时间复杂度为O(n)，其中n表示字符串的长度。算法需要对字符串中的每个字符进行遍历，因此时间复杂度与字符串的长度成正比。
• 空间复杂度为O(1)，因为算法只使用了常数个变量和一个固定大小的哈希表（状态转移规则），不随输入规模的增加而增加额外的空间消耗。因此，算法的空间复杂度是常数级别的。

LeetCode运行结果：

方法二：正则表达式

除了有限状态自动机，还可以使用正则表达式来判断一个字符串是否为有效数字。Java中提供了一个函数matches(String regex)来判断一个字符串是否能够匹配指定的正则表达式。

class Solution {
public boolean isNumber(String s) {// 使用正则表达式匹配字符串return s.trim().matches("[+-]?(?:\\d+\\.?\\d*|\\.\\d+)(?:[Ee][+-]?\\d+)?");
}
}

复杂度分析：

该算法的时间复杂度为O(1)，因为使用了Java内置函数，时间复杂度是固定的。空间复杂度为O(1)，因为没有使用额外的空间。

需要注意的是，使用正则表达式虽然代码简单易懂，但是性能可能不如有限状态自动机。正则表达式求解的时间复杂度是O(n)，其中n是字符串长度，适用于一些简单的模式匹配。对于复杂模式，引擎会消耗非常多的时间和空间，建议在使用时注意性能问题。

LeetCode运行结果：

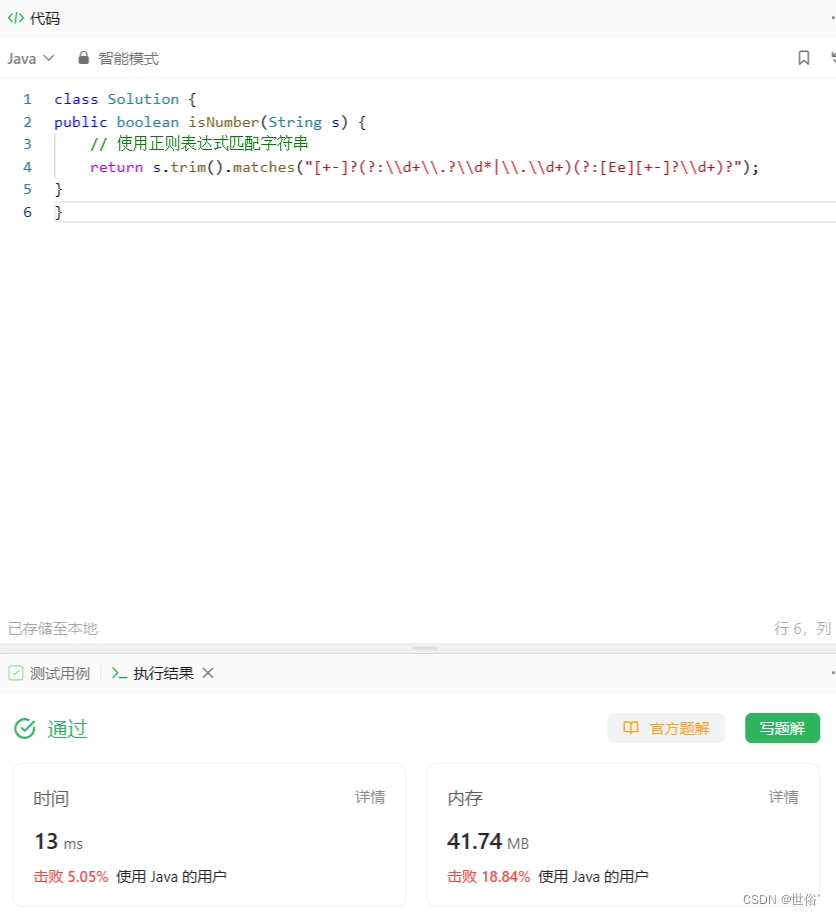
第三题

题目来源

66. 加一 - 力扣（LeetCode）

题目内容

解决方法

方法一：从最后一位向前遍历

该方法从数组的最后一位开始向前遍历，将当前位加一，如果加一后不需要进位，则直接返回结果。如果加一后需要进位，则将当前位置为0，并继续处理前一位。如果所有位都需要进位，则返回新的结果数组，长度为原数组长度加一，首位为1，其余位为0。

class Solution {
public int[] plusOne(int[] digits) {int n = digits.length;// 从最后一位开始向前遍历for (int i = n - 1; i >= 0; i--) {// 当前位加一digits[i]++;// 如果当前位加一后仍然小于10，没有进位，直接返回结果if (digits[i] < 10) {return digits;}// 有进位，当前位变为0，继续处理前一位digits[i] = 0;}// 若所有位都有进位，则数组长度需要增加1，首位为1，后面全是0int[] result = new int[n + 1];result[0] = 1;return result;
}}

复杂度分析：

• 时间复杂度：O(n)，其中n为数组的长度。在最坏情况下，需要遍历整个数组一次。
• 空间复杂度：O(n)，需要创建一个新的结果数组，长度可能为n+1。

LeetCode运行结果：

方法二：数学运算

还可以使用数学运算来实现加一操作。

1. 首先将数组最后一位加一，记录进位carry。
2. 从数组倒数第二位开始，将当前位加上进位carry，并更新进位carry。
3. 如果进位carry为0，则无需继续处理，直接返回结果数组。
4. 如果进位carry不为0，则继续向前处理前一位。
5. 如果处理完所有位后，进位carry仍然不为0，说明需要扩展结果数组的长度，将原数组复制到新的结果数组中，并在首位插入进位carry。

class Solution {
public int[] plusOne(int[] digits) {int n = digits.length;int carry = 1; // 进位初始化为1// 从数组最后一位开始计算for (int i = n - 1; i >= 0; i--) {digits[i] += carry; // 当前位加上进位carry = digits[i] / 10; // 计算新的进位digits[i] %= 10; // 当前位取模，得到个位数// 如果进位为0，说明不需要再进位，直接返回结果数组if (carry == 0) {return digits;}}// 若所有位都有进位，则数组长度需要增加1，首位为进位carry，后面全是0int[] result = new int[n + 1];result[0] = carry;System.arraycopy(digits, 0, result, 1, n);return result;
}}

复杂度分析：

• 时间复杂度：遍历数组需要线性时间O(n)，其中每个元素只进行一次常数级别的数学运算，所以总体时间复杂度也是O(n)。
• 空间复杂度：除了原数组外，需要在进位的情况下创建一个新数组来存储结果，所以空间复杂度为O(n)。

LeetCode运行结果：