狗爹服务器做视频网站百度收录提交工具
Spatial Data Analysis(六):空间优化问题
使用pulp库解决空间优化问题:
pulp是一个用于优化问题的Python库。它包含了多种优化算法和工具,可以用于线性规划、混合整数线性规划、非线性规划等问题。Pulp提供了一个简单的方式来定义优化问题,包括变量、约束和目标函数,并且可以使用多种求解器进行求解。Pulp也提供了可视化工具来展示优化问题的结果。Pulp是一个开源项目,可以在GitHub上获取它的源代码。
空间优化(一):p-中值问题
这个问题需要p设施的位置,同时最小化服务所有需求的总加权距离。
每个节点都有一个关联的权重,表示该节点的需求量。
目标函数: 最小化所有设施和需求节点的需求加权总和。
决策变量: 将设施放置在何处以及哪个设施位置为哪些需求节点提供服务
限制:
- 每个节点由 1 个设施提供服务
- 仅当某个位置存在设施时,节点才可以由该设施提供服务。
- 我们必须放置p设施
- 每个节点要么是一个设施,要么不是。
pip install -q pulp
from pulp import *
import numpy as np
import geopandas as gp
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
#read a sample shapefile
georgia_shp = gp.read_file("https://raw.githubusercontent.com/Ziqi-Li/GEO4162C/main/data/georgia/G_utm.shp")
georgia_shp.shape
(172, 18)
创建一个需求和一个设施变量,表示每个需求和设施的索引。
需求节点:所有县
facility:设施将建在一些选定的县之上
#create a demand and a facilities variable, indicating the indices of each demand and facility.
#demand node: all counties
#facility: Facilities will be built on top of some chosen countiesdemand = np.arange(0,172,1)
facilities = np.arange(0,172,1)
计算距离矩阵d_ij(n×n)
#Calculate a distance matrix d_ij (n by n)
coords = list(zip(georgia_shp.centroid.x,georgia_shp.centroid.y))d = cdist(coords,coords)
每个县(hi)的需求是总人口
#the demand for each county (h_i) is the total populatoion
h = georgia_shp.TotPop90.values
声明设施变量;生成的变量名称为:X_1,X_2,…
# declare facilities variables;the resulting variable names are: X_1,X_2,...
X = LpVariable.dicts('X_%s',(facilities),cat='Binary')# declare demand-facility pair variables; the resulting variable names are Y_0_1, Y_0_2,...
Y = LpVariable.dicts('Y_%s_%s', (demand,facilities),cat='Binary')
要放置的设施数量
#Number of facilities to place
p = 3 #change this and re-run the code.#Create a new problem
prob = LpProblem('P_Median', LpMinimize)
目标函数:最小化所有设施和需求节点的加权需求距离总和
(h_i: i 处的需求;d_ij: i 和 j 之间的距离)
“for”循环用于迭代序列
# Objective function: Minimizing weighted demand-distance summed over all facilities and demand nodes
# (h_i: demand at i; d_ij: distance between i and j)
# A "for" loop is used for iterating over a sequenceprob += sum(sum(h[i] * d[i][j] * Y[i][j] for j in facilities) for i in demand)
这个约束表明我们必须精确放置 p 个设施
# This constraint indicates we must place exactly p facilitiesprob += sum([X[j] for j in facilities]) == p
这一约束意味着需求节点 i 只能由一个设施提供服务
# This constraint implies that a demand node i can only be serviced by one facilityfor i in demand:prob += sum(Y[i][j] for j in facilities) == 1
这个约束意味着需求节点 i
仅当 j 处有设施时才能由 j 处的设施提供服务
它隐式地消除了 X[j] = 0 但 Y[i][j] = 1 时的情况
(节点 i 由 j 提供服务,但 j 处没有设施)
# This constraint implies that that demand node i
# can be serviced by a facility at j only if there is a facility at j
# It implicitly removes situation when X[j] = 0 but Y[i][j] = 1
# (node i is served by j but there is no facility at j)for i in demand:for j in facilities:prob += Y[i][j] <= X[j]
%%time# Solve the above problem
prob.solve()print("Status:", LpStatus[prob.status])
Status: Optimal
CPU times: user 1.35 s, sys: 64 ms, total: 1.42 s
Wall time: 11.5 s
# The minimized total demand-distance. The unit is person * meter (total distance travelled)
print("Objective: ",value(prob.objective))
Objective: 469538765110.4489
# Print the facility node.
rslt=[]
for v in prob.variables():subV = v.name.split('_')if subV[0] == "X" and v.varValue == 1:rslt.append(int(subV[1]))print('Facility Node: ', subV[1])
Facility Node: 126
Facility Node: 30
Facility Node: 82
# Get the geomerty of the facility nodes.
fac_loc = georgia_shp.iloc[rslt,:]
fac_loc
| AREA | PERIMETER | G_UTM_ | G_UTM_ID | AREANAME | Latitude | Longitud | TotPop90 | PctRural | PctBach | PctEld | PctFB | PctPov | PctBlack | X | Y | AreaKey | geometry | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 126 | 7.315030e+08 | 117190.0 | 130 | 128 | GA, Crisp County | 31.92540 | -83.77159 | 20011 | 48.4 | 10.0 | 12.47 | 0.30 | 29.0 | 40.66 | 805648.4 | 3537103 | 13081 | POLYGON ((787012.250 3547615.750, 820243.312 3... |
| 30 | 1.385270e+09 | 274218.0 | 32 | 31 | GA, Fulton County | 33.78940 | -84.46716 | 648951 | 4.2 | 31.6 | 9.63 | 4.13 | 18.4 | 49.92 | 733728.4 | 3733248 | 13121 | POLYGON ((752606.688 3785970.500, 752835.062 3... |
| 82 | 9.179670e+08 | 121744.0 | 84 | 84 | GA, Jenkins County | 32.78866 | -81.96042 | 8247 | 53.8 | 7.7 | 13.10 | 0.21 | 27.8 | 41.51 | 970465.7 | 3640263 | 13165 | POLYGON ((989566.750 3653155.750, 981378.062 3... |
#Plot the faclities (stars) on top of the demand map.
fig, ax = plt.subplots(figsize=(5,5))georgia_shp.centroid.plot(ax=ax,markersize=georgia_shp.TotPop90/1000)#markersize is proportional to the population
fac_loc.centroid.plot(ax=ax,color="red",markersize=300,marker="*")

空间优化(二):集合覆盖问题
在此模型中,设施可以为距设施给定覆盖距离 Dc 内的所有需求节点提供服务。 问题在于放置最少数量的设施,以确保所有需求节点都能得到服务。 我们假设设施没有容量限制。
pip install -q pulp
from pulp import *
import numpy as np
import geopandas as gp
from scipy.spatial.distance import cdistimport matplotlib.pyplot as plt
#read a sample shapefile
georgia_shp = gp.read_file("https://raw.githubusercontent.com/Ziqi-Li/GEO4162C/main/data/georgia/G_utm.shp")
georgia_shp.shape
(172, 18)
创建一个需求和一个设施变量,表示每个需求和设施的索引。
需求节点:所有县
facility:我们可以在一些县建造设施
#create a demand and a facilities variable, indicating the indices of each demand and facility.
#demand node: all counties
#facility: we could build facilities in some countiesdemand = np.arange(0,172,1)
facilities = np.arange(0,172,1)
计算距离矩阵d_ij(n×n)
#Calculate a distance matrix d_ij (n by n)
coords = list(zip(georgia_shp.centroid.x,georgia_shp.centroid.y))
d = cdist(coords,coords)
阈值覆盖距离
# Threshold coverage distance
Dc = 100000 #100km coverage, change this and re run the code.
创建一个变量,指示节点 i 是否可以被设施 j 覆盖。
#Creata a variable (alpha in the lecture slide pg.28), indicating whether a node i can be covered by facility j.
a = np.zeros(d.shape)
a[d <= Dc] = 1
a[d > Dc] = 0
声明设施变量 Xj
# declare facilities variables Xj
X = LpVariable.dicts('X_%s',(facilities),cat='Binary')
创建一个最小化问题
#Create an minimization problem
prob = LpProblem('Set_Covering', LpMinimize)
目标函数:我们要最小化放置设施的数量
# Objective function: we want to minimize the number of placed facilities
prob += sum([X[j] for j in facilities])
该约束意味着每个需求节点 i 需要至少由设施服务
# This constraint implies every demand node i needs to be served by at least facility
for i in demand:prob += sum(a[i][j]*X[j] for j in facilities) >= 1%%time
# Solve the above problem
prob.solve()print("Status:", LpStatus[prob.status])
Status: Optimal
CPU times: user 22.5 ms, sys: 1.05 ms, total: 23.6 ms
Wall time: 66.4 ms
# The minimal number of facilities with the defiened coverage.
print("Objective: ",value(prob.objective))
Objective: 8.0
# Print the facility nodes.
rslt = []
for v in prob.variables():subV = v.name.split('_')if subV[0] == "X" and v.varValue == 1:rslt.append(int(subV[1]))print('Facility Node: ', subV[1])
Facility Node: 102
Facility Node: 120
Facility Node: 145
Facility Node: 150
Facility Node: 30
Facility Node: 38
Facility Node: 9
Facility Node: 97
# Get the geomerty of the facility nodes.
fac_loc = georgia_shp.iloc[rslt,:]
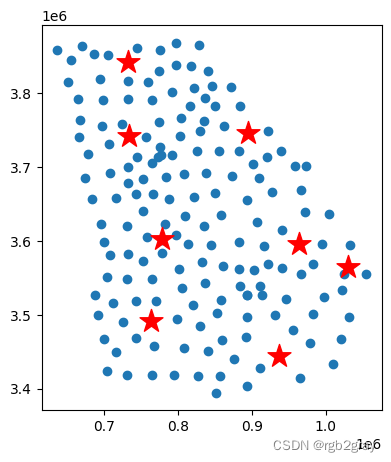
#Plot the faclities (stars) on top of the demand map.
fig, ax = plt.subplots(figsize=(5,5))georgia_shp.centroid.plot(ax=ax)
fac_loc.centroid.plot(ax=ax,color="red",markersize=300,marker="*")
<Axes: >