深圳网站建设 案例下载百度2023最新版
1.数理逻辑
2. 集合论
3. 代数系统
4. 图论
代数系统:把一些形式上很不相同的代数系统,用统一的方法描述、研究、推理,从而得到反映出他们共性的一些结论,在将结论运用到具体的代数系统中
系统:运算+研究对象
- 运算:具有的共同性质的不同演算抽取成一个运算,根据性质的不同取名群、环域等。
- 研究对象:可以运算的抽象对象
如:集合上的并满足结合律,实数上的加法也满足结合律,用一个符号代表具有结合律的运算,而研究对象变为代表实数或者集合等对象的抽象事物
所以代数系统定义为:非空集合和定义在集合上的封闭运算构成的系统
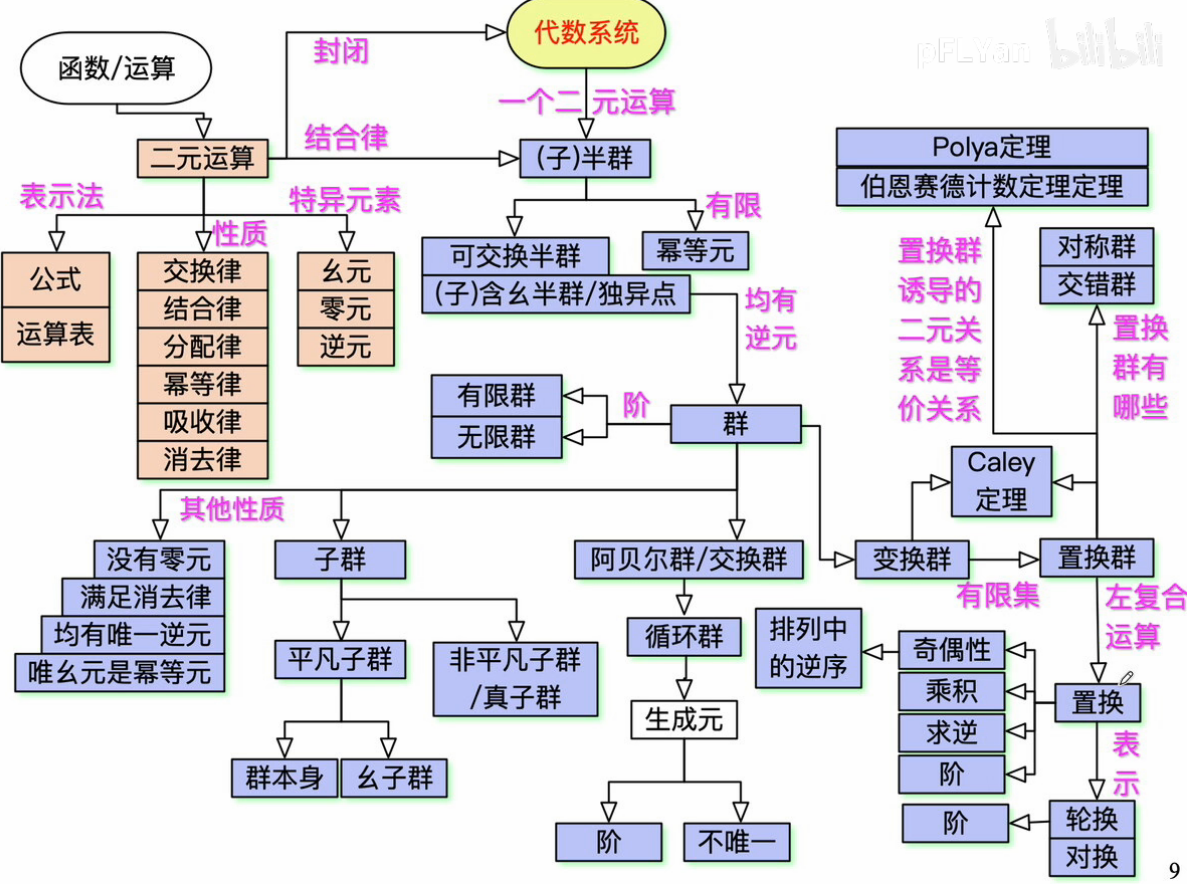
5. 代数系统
5.0 代数学
代数学:研究数的部分
几何学:研究形的部分
分析学:沟通数与性且设计极限运算的部分
代数:用字母代替具体的数值
发展历程
-
算数
-
初等代数
-
代数式的运算、方程
从简单的一元一次方程开始
讨论二元和三元的一次方程
研究二元以上及可以转换为二元的方程组
-
数与方程理论
- 无理数与有理数的界定
- 运算符号的创立与无理方程的解法
- 虚数理论
-
高等代数
-
线性代数:讨论任意多个未知数的一元方程组(线性方程组)
费马与笛卡尔引入笛卡尔坐标系,统一了代数与集合,线性代数才出现
仅涉及线性运算(加法和数乘)的代数学分支,以矩阵为研究工具,以向量空间和线性映射为研究对象
-
多项式代数:研究更高次的一元方程组
-
-
(19世纪以后)抽象代数
系统:将不同演算共有的性质抽取形成系统,根据抽取的性质取名群、环域等。
如:集合上的并有结合律,实数上的加法也有结合律,用一个符号代表具有结合律的运算,而研究对象变为代表实数或者集合等对象的抽象事物
所以代数系统定义为:抽象的研究对象集合和满足某种性质的运算构成的系统
具体应用:
伽罗瓦用置换群的方法证明一般形式的一元五次方程没有通解,给出了可解性的判别原则
格与布尔代数:用于电子线路设计、电子计算机硬件设计和通信系统设计
半群:形式语言,自动机理论
5.1 运算
5.1.1 运算的概念
二元运算:函数 f:A×A→Af:A\times A\rightarrow Af:A×A→A,则称f为A上的二元代数运算
如:
-
加法与乘法是在 Z+Z^+Z+ 上的二元代数运算,运算结果也是 Z+Z^+Z+ ,所以是封闭的
f(<x,y>)=x+y,x∈Z+,y∈Z+,x+y∈Z+f(<x,y>)=x+y,x\in Z^+,y\in Z^+,x+y\in Z^+f(<x,y>)=x+y,x∈Z+,y∈Z+,x+y∈Z+
-
减法不是 Z+Z^+Z+ 上的二元运算,因为 x−y∉?Z+x-y\notin^{?} Z^+x−y∈/?Z+ ,所以是不封闭的
-
减法在Z上是二元运算,x−y∈Zx-y\in Zx−y∈Z ,是封闭的
5.1.2 运算的性质
二元运算 A×A→AA\times A\rightarrow AA×A→A 上的性质,以*为运算符
交换律
∀x,y∈A,有x∗y=y∗x,称∗满足交换律\forall x,y\in A,有x*y=y*x,称 *满足交换律 ∀x,y∈A,有x∗y=y∗x,称∗满足交换律
运算表关于主对角线对称
结合律
∀x,y,z∈A,有(x∗y)∗z=x∗(y∗z),称∗满足结合律\begin{aligned} \forall x,y,z\in A,有(x*y)*z=x*(y*z),称*满足结合律 \end{aligned} ∀x,y,z∈A,有(x∗y)∗z=x∗(y∗z),称∗满足结合律
分配律
∀x,y,z∈A,有{x∗(y⋅z)=x∗y⋅x∗z(y⋅z)∗x=y∗x⋅z∗x,则称∗满足分配律\forall x,y,z\in A,有\begin{cases} x*(y·z)=x*y·x*z\\ (y·z)*x=y*x·z*x \end{cases} ,则称*满足分配律 ∀x,y,z∈A,有{x∗(y⋅z)=x∗y⋅x∗z(y⋅z)∗x=y∗x⋅z∗x,则称∗满足分配律
幂等律
∀x∈A,有x∗x=x,则称∗满足幂等律若∃a∈A,且a∗a=a,则称a是∗的幂等元\begin{aligned} &\forall x\in A,有x*x=x,则称*满足幂等律\\ &若\exists a\in A,且a*a=a,则称a是*的幂等元 \end{aligned} ∀x∈A,有x∗x=x,则称∗满足幂等律若∃a∈A,且a∗a=a,则称a是∗的幂等元
主对角线元素排列与表头顺序一直
吸收律
∀x,y∈A,有{x∗(x⋅y)=xx⋅(x∗y)=x,则称∗和⋅满足吸收律\forall x,y \in A,有 \begin{cases} x*(x·y)=x\\ x·(x*y)=x \end{cases}, 则称*和·满足吸收律 ∀x,y∈A,有{x∗(x⋅y)=xx⋅(x∗y)=x,则称∗和⋅满足吸收律
消去律
若满足两个关系:{x∗y=x∗z(x≠0),则y=zy∗x=z∗x(x≠0),则y=z,∗满足消去律若满足两个关系: \begin{cases} x*y=x*z(x\neq 0),则y=z\\ y*x=z*x(x\neq 0),则y=z \end{cases} ,*满足消去律 若满足两个关系:{x∗y=x∗z(x=0),则y=zy∗x=z∗x(x=0),则y=z,∗满足消去律
Z上的加法、乘法满足消去律
幂集 ρ(A)\rho(A)ρ(A) 上的 U 不满足消去律
- A∪B=A∪C⇏B=CA\cup B=A\cup C \nRightarrow B=CA∪B=A∪C⇏B=C
5.1.3 表示方法
- 公式
- 运算表
5.2 代数系统
5.2.1 基本概念
代数系统:非空集合A和A上的k个封闭的运算 f1,f2,...,fkf_1,f_2,...,f_kf1,f2,...,fk 组成的系统,称为一个代数系统,记作 <A,f1,f2,...,fk><A,f_1,f_2,...,f_k><A,f1,f2,...,fk>
如: <R,+>,<R,∗>,<ρ(A),∪,∩><R,+>,<R,*>,<\rho(A),\cup,\cap><R,+>,<R,∗>,<ρ(A),∪,∩>
子代数系统:设 <A,∗1,∗2,...,∗k><A,*_1,*_2,...,*_k><A,∗1,∗2,...,∗k> 是代数系统,若 B⊆A,B≠∅B\subseteq A,B\neq ∅B⊆A,B=∅ ,且运算 ∗1,∗2,...,∗k*_1,*_2,...,*_k∗1,∗2,...,∗k 对B是封闭的,则 <B,∗1,∗2,...,∗k><B,*_1,*_2,...,*_k><B,∗1,∗2,...,∗k> 也是代数系统,称为 <A,∗1,∗2,...,∗k><A,*_1,*_2,...,*_k><A,∗1,∗2,...,∗k> 的子代数系统
若 B⊂AB\subset AB⊂A,则称 <B,∗1,∗2,...,∗k><B,*_1,*_2,...,*_k><B,∗1,∗2,...,∗k> 为真子代数系统
如:
对<R,−>:<Z,−>是<R,−>的真子代数系统<N,−>不是<R,−>的真子代数系统对<R,->: \begin{aligned} &<Z,->是<R,->的真子代数系统\\ &<N,->不是<R,->的真子代数系统 \end{aligned} 对<R,−>:<Z,−>是<R,−>的真子代数系统<N,−>不是<R,−>的真子代数系统
5.2.2 特殊元
幺元零元
代数系统的幺元,零元 ,若存在必唯一
左幺元:设*是S上的二元运算,1l1_l1l 是S中的元素,如果对S中的每一元素x,有1l∗x=x1_l*x=x1l∗x=x,则称 1l1_l1l 是对运算 * 的左幺元
左零元:如果对于S中的每个元素x,有 0l∗x=0l0_l*x=0_l0l∗x=0l ,则称 0l0_l0l 对运算 * 是左零元
设 * 是S上的二元运算,1是S中的元素,对于S中的每个元素,满足 1∗x=x∗1=x1*x=x*1=x1∗x=x∗1=x ,则1为对运算 * 的幺元。
如果对于S中的每一元素x,有 0∗x=x∗0=00*x=x*0=00∗x=x∗0=0 ,则称0对运算 * 是零元
- 在运算表中
- 幺元:所在的行与列的元素排列都与表头一致
- 零元:元素的行与列都有钙元素自身构成
逆元
某个元素的逆元
设 * 是S上的二元运算,1是对运算 * 的幺元。如果 x*y =1,那么关于运算 * ,x是y的左逆元,y是x的右逆元
如果 x*y=1和y*x=1都成立,则关于运算 *,x是y的逆元
x的逆元记作 x−1x^{-1}x−1 ,存在逆元的元素称为可逆的

5.3 含一个运算的代数系统
5.3.1 半群
设 V=<S,∗>V=<S,*>V=<S,∗> 是代数系统,* 为一个二元运算符
- 若 * 是可结合的,则称V是半群
如:乘法,加法,关系的合成,<ρ(A),∪>,<ρ(A),∩><\rho(A),\cup>,<\rho(A),\cap><ρ(A),∪>,<ρ(A),∩> 都是半群
幂等元:∃a∈S,使得a2=a\exists a\in S,使得 a^2=a∃a∈S,使得a2=a 成立,则称a是幂等元素
-
定理:有限半群必有幂等元
连续幂等后根据封闭性,结果仍在集合中,所以一定存在幂等元
子半群
在非空子集上的运算是封闭的半群
独异点(含幺半群)
含幺半群=半群+幺元
半群V中 * 运算符含有幺元,则称V是含幺半群(独异点),记作 <S,∗,1><S,*,1><S,∗,1>
如:矩阵乘法
证明独异点
在R中定义二元运算 * ,∀a,b∈R,a∗b=a+b+ab\forall a,b \in R,a*b=a+b+ab∀a,b∈R,a∗b=a+b+ab ,求证 <R,∗><R,*><R,∗> 构成独异点
1.∀a,b∈R,a∗b=a+b+ab∈R,所以∗是封闭的即<R,∗>是一个代数系统2.(a∗b)∗c=(a∗b)+c+(a∗b)c=(a+b+ab)+c+(a+b+ab)c=a+b+c+ab+ac+bc+abcc∗(a∗b)=c+(a∗b)+c(a∗b)=c+(a+b+ab)+c(a+b+ab)=a+b+c+ab+ac+bc+abc所以∗是可结合的,故<R,∗>是半群3.对0∈R,∀x∈R,有0∗x=x=x∗0=x,所以0为幺元综上,<R,∗>是独异点\begin{aligned} 1.\quad &\forall a,b \in R,a*b=a+b+ab\in R,所以*是封闭的\\&即<R,*>是一个代数系统\\ 2.\quad &(a*b)*c=(a*b)+c+(a*b)c=(a+b+ab)+c+(a+b+ab)c\\&=a+b+c+ab+ac+bc+abc\\ &c*(a*b)=c+(a*b)+c(a*b)=c+(a+b+ab)+c(a+b+ab)\\&=a+b+c+ab+ac+bc+abc\\ &所以 *是可结合的,故<R,*>是半群\\ 3.\quad &对0\in R,\forall x\in R,有0*x=x=x*0=x,所以0为幺元\\ &综上,<R,*>是独异点 \end{aligned} 1.2.3.∀a,b∈R,a∗b=a+b+ab∈R,所以∗是封闭的即<R,∗>是一个代数系统(a∗b)∗c=(a∗b)+c+(a∗b)c=(a+b+ab)+c+(a+b+ab)c=a+b+c+ab+ac+bc+abcc∗(a∗b)=c+(a∗b)+c(a∗b)=c+(a+b+ab)+c(a+b+ab)=a+b+c+ab+ac+bc+abc所以∗是可结合的,故<R,∗>是半群对0∈R,∀x∈R,有0∗x=x=x∗0=x,所以0为幺元综上,<R,∗>是独异点
定理
- x,y都有逆元,则 x*y 有逆元,且 (x∗y)−1=x−1∗y−1(x*y)^{-1}=x^{-1}*y^{-1}(x∗y)−1=x−1∗y−1
可交换半群=半群+满足交换律
若半群 V=<S,∗>V=<S,*>V=<S,∗> 的运算符 * 是可交换的,V是可交换半群
定理
- 在可交换半群 <S,∗><S,*><S,∗> 中,有 (a∗b)n=an∗bn(a*b)^n=a^n*b^n(a∗b)n=an∗bn ,其中n是正整数, a,b∈Sa,b\in Sa,b∈S
独异点 <S,∗,1><S,*,1><S,∗,1> 中的 * 是可交换的,称V是可交换独异点
循环半群=半群+生成元
5.3.2 群
群=含幺半群+每个元素有逆元
设 V=<S,∗>V=<S,*>V=<S,∗> 是代数系统,* 是二元运算
若 * 是可结合的,存在幺元 ∃1∈S\exists 1 \in S∃1∈S ,且 ∀x∈S,有x−1∈S\forall x\in S,有x^{-1}\in S∀x∈S,有x−1∈S ,称V为群
如:
<N,+>满足结合律,所以是半群。幺元是0,所以是含幺半群。但是<N,+>不是群,每个元素的逆不在N中\begin{aligned} &<N,+>满足结合律,所以是半群。幺元是0,所以是含幺半群。但是\\ &<N,+>不是群,每个元素的逆不在N中 \end{aligned} <N,+>满足结合律,所以是半群。幺元是0,所以是含幺半群。但是<N,+>不是群,每个元素的逆不在N中
证明群的过程
设Z为整数集合,在Z上定义二元运算*,∀x,y∈Z\forall x,y\in Z∀x,y∈Z,x*y=x+y-2,为 <Z,∗><Z,*><Z,∗> 是否为群
1.∀x,y∈Z,x∗y=x+y−2∈Z,所以∗是封闭的,即<Z,∗>是代数系统2.∀x,y,z∈Z(x∗y)∗z=(x+y−2)+z−2=x+y+z−4x∗(y∗z)=x+(y+z−2)−2=x+y+z−4即∗是可结合的,所以<Z,∗>是半群3.设p是幺元,p∗x=p=p+x−2=x⇒p=2故半群<R,∗>是独异点,幺元为24.x∗x−1=2⟺x+x−1=4⇒x−1=4−x∈Z故<R,∗>是群\begin{aligned} 1.\quad &\forall x,y\in Z,x*y=x+y-2\in Z,所以*是封闭的,即<Z,*>是代数系统\\ 2.\quad &\forall x,y,z\in Z \\ &(x*y)*z=(x+y-2)+z-2=x+y+z-4\\ &x*(y*z)=x+(y+z-2)-2=x+y+z-4\\ &即*是可结合的,所以<Z,*>是半群\\ 3.\quad &设p是幺元,p*x=p=p+x-2=x\Rightarrow p=2\\ &故半群<R,*>是独异点,幺元为2\\ 4.\quad &x*x^{-1}=2\iff x+x^{-1}=4\Rightarrow x^{-1}=4-x\in Z\\ &故<R,*>是群 \end{aligned} 1.2.3.4.∀x,y∈Z,x∗y=x+y−2∈Z,所以∗是封闭的,即<Z,∗>是代数系统∀x,y,z∈Z(x∗y)∗z=(x+y−2)+z−2=x+y+z−4x∗(y∗z)=x+(y+z−2)−2=x+y+z−4即∗是可结合的,所以<Z,∗>是半群设p是幺元,p∗x=p=p+x−2=x⇒p=2故半群<R,∗>是独异点,幺元为2x∗x−1=2⟺x+x−1=4⇒x−1=4−x∈Z故<R,∗>是群
有限群&无限群
设 <G,∗><G,*><G,∗> 是一个群
-
如果G是有限集,则称 <G,∗><G,*><G,∗> 是有限群,G中的元素个数称为群的阶,记为 ∣G∣\mid G \mid∣G∣
-
G是无限集,则为无限群,群的阶为无限
群的基本性质
二阶以上的群无零元
- 一阶群一定有零元,零元即幺元, <g,∗><{g},*><g,∗> g*g=g,所以g是零元
群中每个元素都存在唯一逆元
群中除幺元外无幂等元
群的运算表中,没有两行或两列是相同的
群满足消去律
满足消去律的有限半群是群
- 没有零元的有限半群是群
子群
设 <G,∗><G,*><G,∗> 为群,H⊆GH\subseteq GH⊆G,且 <H,∗><H,*><H,∗> 为群,则称H为G的子群,记作 H≤GH\le GH≤G
子群判定定理
设 <G,∗><G,*><G,∗> 为群,H是G的非空子集
<H,∗>是<G,∗>的非空子群⟺{封闭:∀a,b∈H,有a∗b∈H逆元:∀a∈H,有a−1∈H⟺∀a,b∈H,有a∗b−1∈HH是G的子集且H是有限集⟺∀a,b∈H,有a∗b∈H\begin{aligned} <H,*>是<G,*>的非空子群 &\iff \begin{cases} 封闭:\forall a,b\in H,有a*b\in H\\ 逆元:\forall a\in H,有a^{-1}\in H \end{cases}\\ &\iff \forall a,b\in H,有a*b^{-1}\in H\\ H是G的子集且H是有限集&\iff \forall a,b\in H,有a*b\in H \end{aligned} <H,∗>是<G,∗>的非空子群H是G的子集且H是有限集⟺{封闭:∀a,b∈H,有a∗b∈H逆元:∀a∈H,有a−1∈H⟺∀a,b∈H,有a∗b−1∈H⟺∀a,b∈H,有a∗b∈H
性质
子群的幺元是群的幺元,∀a∈H\forall a\in H∀a∈H ,其逆元 aH−1a_H^{-1}aH−1 就是a在G中的逆元 a−1a^{-1}a−1
二阶以上的群 <G,∗><G,*><G,∗> 一定存在两个子群,称为G的平凡子群
-
由幺元组成的子群 <1,∗><{1},*><1,∗> 称为G的幺子群,其中 1就是 <G,∗><G,*><G,∗> 的幺元
-
<G,∗><G,*><G,∗> 群本身
-
其余子群称为 非平凡子群/真子群
交换群:满足交换律的群
若群 V=<S,∗>V=<S,*>V=<S,∗> 中的 * 满足交换律,则称V是可交换的群(阿贝尔群)

循环群:有生成元的交换群
群中的每个元素都可用一个元素的方幂表示,则称这个群是循环群
群 V=<G,∗>V=<G,*>V=<G,∗> 中,如果 ∃g∈G\exists g\in G∃g∈G,对于每个元素 a∈Ga\in Ga∈G,都有一个相应的 i∈Ii\in Ii∈I ,能把a表示成幂次 gig^igi 的形式,则称 <G,∗><G,*><G,∗> 是一个循环群。或循环群是由g生成的,g是 <G,∗><G,*><G,∗> 的生成元
循环群的判别
证明:<Z,+><Z,+><Z,+> 是循环群
1.∀a,b∈Z,a+b∈Z,故+是封闭的<G,+>是一个代数系统2.∀a,b,c∈Z,(a+b)+c=a+(b+c)=a+b+c所以<G,+>是半群3.设幺元为p,∀x∈Z,p+x=x,则p=0幺元=04.∀a∈Z,a+a−1=0⇒a−1=−a∈Z所以<G,+>是群5.设g=1,∀n∈Z+,n=1+1+...+1=1n∀n∈Z−,n=(−1)+(−1)+...+(−1)=(−1)n=(1−1)n故1是<G,∗>的生成元,该群为循环群\begin{aligned} &1. \quad \forall a,b\in Z,a+b\in Z,故+是封闭的\\ & \quad <G,+>是一个代数系统\\ &2.\quad \forall a,b,c \in Z,(a+b)+c=a+(b+c)=a+b+c\\ &\quad 所以<G,+>是半群\\ &3.\quad 设幺元为p,\forall x\in Z,p+x=x,则p=0\\ &\quad 幺元=0\\ &4. \quad \forall a\in Z,a+a^{-1}=0\Rightarrow a^{-1}=-a\in Z\\ &\quad 所以<G,+>是群\\ &5. \quad 设g=1,\forall n\in Z_+,n=1+1+...+1=1^{n}\\ &\quad \forall n\in Z_-,n=(-1)+(-1)+...+(-1)=(-1)^n=(1^{-1})^n\\ &故1是<G,*>的生成元,该群为循环群 \end{aligned} 1.∀a,b∈Z,a+b∈Z,故+是封闭的<G,+>是一个代数系统2.∀a,b,c∈Z,(a+b)+c=a+(b+c)=a+b+c所以<G,+>是半群3.设幺元为p,∀x∈Z,p+x=x,则p=0幺元=04.∀a∈Z,a+a−1=0⇒a−1=−a∈Z所以<G,+>是群5.设g=1,∀n∈Z+,n=1+1+...+1=1n∀n∈Z−,n=(−1)+(−1)+...+(−1)=(−1)n=(1−1)n故1是<G,∗>的生成元,该群为循环群
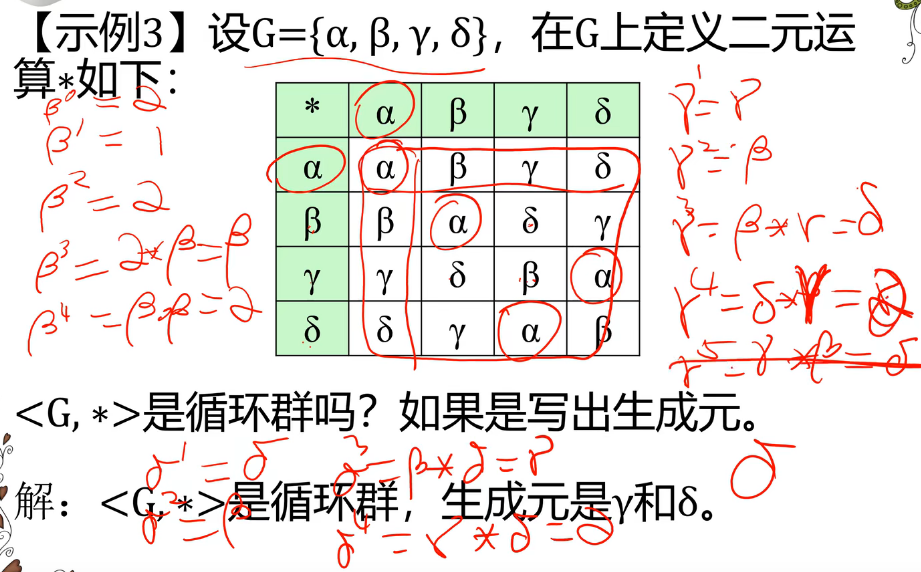
循环群的性质
-
生成元不唯一

-
群的阶:设 <G,∗><G,*><G,∗> 是一个由元素a生成的循环群,且是 有限群,如果G的阶是n,即 ∣G∣=n\mid G \mid=n∣G∣=n ,则 an=1a^n=1an=1 且 G={a,a2,...,an=1}G=\{a,a^2,...,a^n=1\}G={a,a2,...,an=1} ,n是元素 a 的阶(使得 an=1a^n=1an=1 成立的最小正整数)
-
任意的循环群都是交换群

置换群
变换与变换群
变换:在A上的映射/函数
对称群 <SA,◇><S_A,◇><SA,◇>:非空集合A 上的全体 可逆变换(双射函数)的复合运算 构成集合的A的群
- 代数系统——封闭:集合A上的任意两个双射函数复合后仍在集合A中
- 半群——结合律:复合运算具有结合律
- 含幺半群——求幺元:恒等函数,自己到自己的变换
- 群——每个元素逆元都在群中:双射函数的逆元仍在集合中
对称群 <SA,◇><S_A,◇><SA,◇> 的子群称为A的一个变换群
- 运算符号满足结合律,不满足交换律
- 每个群都同构于一个变换群
G是实数集R上 所有变换 fa,b:R→Rf_{a,b}:R\rightarrow Rfa,b:R→R 构成的集合,∀x∈R,fa,b(x)=ax+b\forall x\in R,f_{a,b}(x)=ax+b∀x∈R,fa,b(x)=ax+b , <G,◇><G,◇><G,◇> G是变换群
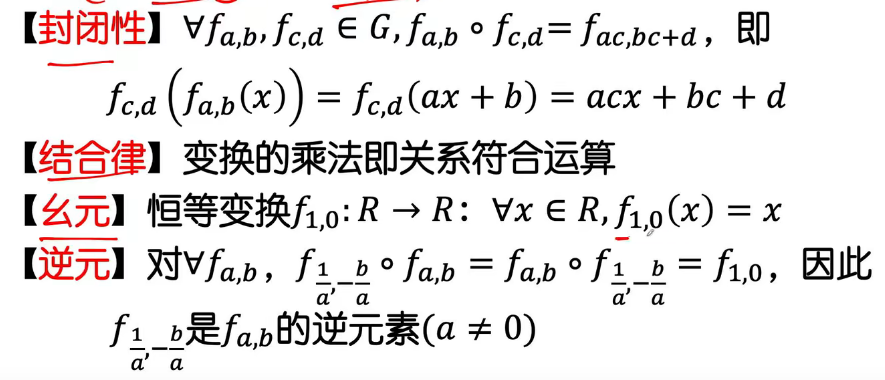
置换
置换:在 有限集合 上的可逆变换(双射函数)
如:集合A={1,2,3,4,5}是有限集合,其上的一个可逆变换(可逆函数/双射函数)即为一个置换
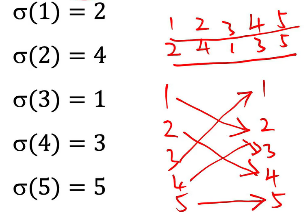
若 ∣A∣=n\mid A \mid=n∣A∣=n ,则A上的置换有 n! 个。A上的所有置换的集合记为 SnS_nSn

置换群
n元有限集合A上的置换所构成的群,称为n元置换群;A上所有置换构成的群称为n次对称群
- 置换群是在 有限集合 上的变换群
- n次对称群是n元置换群的特殊情况
-
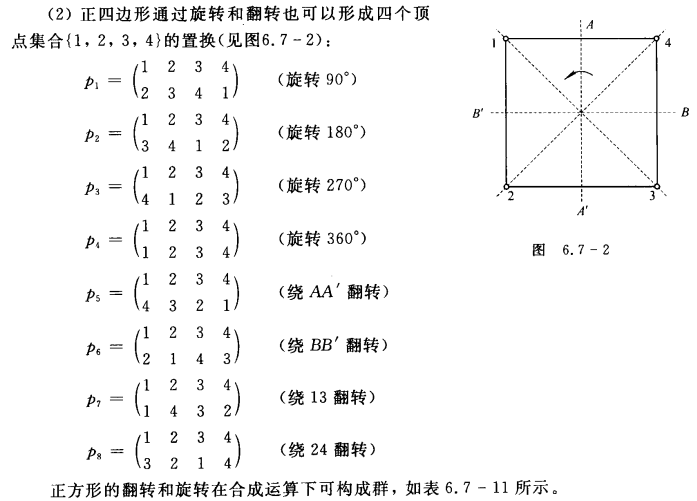
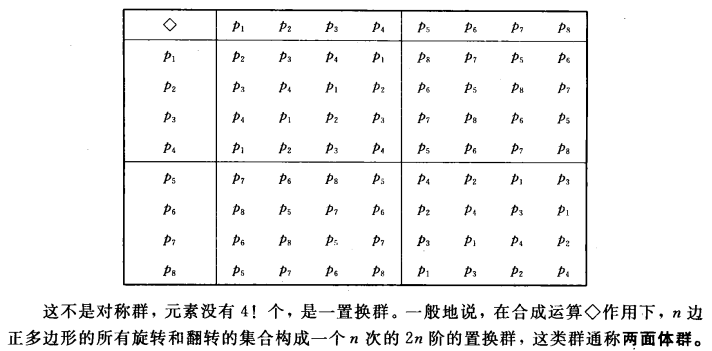
以符号◇表示右合成运算:p1◇p2p_1◇p_2p1◇p2 表示先进行 p1p_1p1 置换,在进行p2p_2p2 置换
-
<Sn,◇><S_n,◇><Sn,◇> 表示对称群,<{p1,p2,...},◇><\{p_1,p_2,...\},◇><{p1,p2,...},◇> 表示置换群
-
任何一个有限群都同构于一个置换群
置换群的几何意义

5.4 含两个运算的代数系统
5.4.1 环
具有两个二元运算的代数系统
设 <R,+,∗><R,+,*><R,+,∗> 是代数系统,+,*为二元运算,若满足
<R,+><R,+><R,+> 是可交换群
<R,∗><R,*><R,∗> 是半群
*对+满足分配律
A*(B+C)=A*B+A*C
称 <G,+,∗><G,+,*><G,+,∗> 为环
整环
若环 <R,+,−><R,+,-><R,+,−> 可交换,含幺元,无零元,称R为整环
对应可交换半群
除环
若环 <R,+,−><R,+,-><R,+,−> 至少存在两个元素,含幺元,无零元,且(逆元也在环中) ∀a∈R(a≠0)\forall a\in R(a\neq 0)∀a∈R(a=0) 有 a−1∈Ra^{-1}\in Ra−1∈R ,称R为除环
对应群
5.4.2 域
若环 <R,+,−><R,+,-><R,+,−> 既是整环又是除环,则称R是域
对应可交换群——阿贝尔群
5.5 格
设 <S,≤><S,\le><S,≤> 是偏序集(自反,反对称,传递),如果 ∀x,y∈S\forall x,y \in S∀x,y∈S ,{x,y} 都有最小上界和最大下界,称S关于 ≤\le≤ 构成一个格,记为:
格<S,≤>,格<S,∧,∨>格<S,\le>,格<S,∧,∨>格<S,≤>,格<S,∧,∨> ,
其中 ∨表示最小上界,∧表示最大下界
每个全序集都是一个格
5.5.1 格的判断
1.
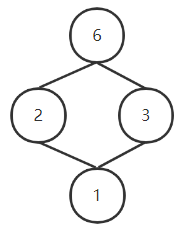
设 <S6,D><S_6,D><S6,D> ,D表示整除,SnS_nSn 表示整除n的因子集合
其中:
1∨2=2,,1∨3=3,1∨6=6,2∨3=6
1∧2=1,,1∧3=1,1∧6=1,2∧3=1
所以是格
2.
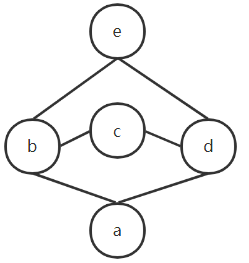
对于 b,d 有最小上界 b∨d=c,e
对于 c,e 有最大下界 c∧e =b,d 但是无最小上界,c与e大小无法判断
所以不是格
3.<ρ(B),⊆><\rho(B),\subseteq><ρ(B),⊆>
∀x,y∈ρ(B),x∨y=x∪y,x∧y=x∩y\forall x,y\in \rho(B),x∨y=x\cup y,x∧y=x\cap y ∀x,y∈ρ(B),x∨y=x∪y,x∧y=x∩y
所以是格
5.5.2 格的界
全界:
若格 <L,∧,∨><L,∧,∨><L,∧,∨> 中 ∃a\exists a∃a,对 ∀b∈L\forall b\in L∀b∈L ,有 a≤b(b≤a)a\le b(b\le a)a≤b(b≤a) ,则称a为格L的全下界(全上界)
全下界a是L中的最小值,哈斯图的最底层一个元素。
全上界a是L中的最大值,哈斯图的最顶层一个元素
5.5.3 特殊的格
有界格
记为:<L,∧,∨,0,1><L,∧,∨,0,1><L,∧,∨,0,1> 。界的位置与运算符号位置对应
有补格
每个元素都有补元,为有补格
补元
有界格 <L,∧,∨,0,1><L,∧,∨,0,1><L,∧,∨,0,1> ,∀a∈L\forall a\in L∀a∈L ,若 ∃b∈L\exists b\in L∃b∈L ,使 a∧b=0,a∨b=1,则称 b是a的 补元
如:
<S8,D><S_8,D><S8,D> ,其哈斯图为:
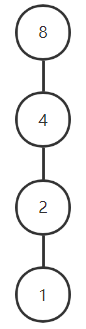
1是全下界,8是全上界,即表示为格 <S8,D,∧,∨,1,8><S_8,D,∧,∨,1,8><S8,D,∧,∨,1,8>。
由于1∧8=1,1∨8=8,所以1和8互为补元
由于1∧2=1,1∨2=2;2∨4=4;2∨8=8,2∧8=2,所以2无补元,同理4无补元
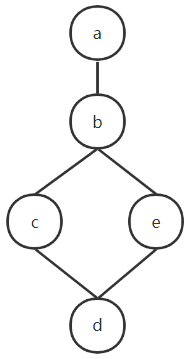
所给哈斯图是格,a为全上界,d为全下界。a与d互为补元,b,c,e无补元
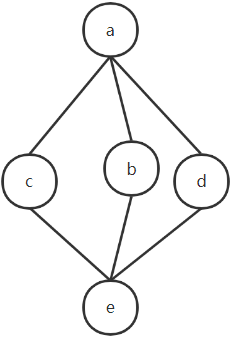
a为全上界,e为全下界,所以a与e互为补元
对于b,c,b∧c=e,b∨c=a,所以b与c互为补元
同理,c与d,b与d互为补元
有界有补分配格
格 <L,∧,∨,0,1><L,∧,∨,0,1><L,∧,∨,0,1> 是有补分配格,称L为布尔代数
-
有界格
-
有补格
-
求界可分配
∧对∨可分配
∨对∧可分配
-
0:全下界
-
1:全上界
如:
<B,∧,∨,′,0,1><B,∧,∨,',0,1><B,∧,∨,′,0,1> 是布尔代数
若a’是a的补元,则a∧a’=0,a∨a’=1
a∨0=a,a∧0=0,a∨1=a,a∧1=a
5.6 代数间的关系
用于研究两个代数系统间的联系
5.6.1 同构
两个代数系统 A=<S,∗,+,k>A=<S,*,+,k>A=<S,∗,+,k> 和 A′=<S′,∗′,+′,k′>A'=<S',*',+',k'>A′=<S′,∗′,+′,k′> ,其中*是二元运算,+是一元运算。若存在一个双射函数h,使
h: S→S′S\rightarrow S'S→S′
h(a*b)=h(a)*'h(b)
h(+a)=+'h(a)
h(k)=k’
则将h为从A到A’的同构
