前言

本章节内容主要做一个全局算法题导航指引，含有代码基本模板、相对应习题以及相关知识点，所有题目围绕这个导航索引进行补充扩展，目前博主水平有限也在不断学习更新当前博客内容。

所有博客文件目录索引：博客目录索引(持续更新)

导航

OI Wiki：我愿称之为算法最全知识点合集！

对于Java的一些注意事项以及API可见：算法竞赛Java选手的语言快速熟悉指南

时间复杂度：

• n ∈ 1000：O(n²)，dp
• n ∈ 10000：O(nlogn)，二分、排序
  • 2¹⁰=1024，2²⁰=1048576（10⁶），2³⁰=1073741824（10⁹），2⁴⁰=1e12，2⁵⁰=1e15。【2²⁰约等于100万，2³¹就爆一秒了】
  • 10! = 362万，11! = 3900万，12! = 4亿，13! = 60亿

关于数据类型以及对应的内存范围：

• int：最大2147483647，20亿，2x10¹⁰
• long：占8个字节，64位，[-9223372036854775808到9223372036854775807] 百亿亿，9*2¹⁹
  • 1亿亿等于1兆，一百兆。
• 64MB：64MB最多可以开16777216个int ，相当于一千六百七十万个。

调试技巧：

①acwing官网问题

• 若是出现Segmentation fault，那么可以使用exit(0)来进行调试确定在哪一行出了错：

void func(){exit(0);
}//调用
func();

• 若是在func()放在当前行执行没有出现Segmentation fault，说明再此之前没有可能出现Segmentation fault，那么就可以将func放置到后面。

②关于输入输出

//输入、输出函数
static BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));

③自定义类及属性 > 定义一维数组效率。具体可见leetcode1235题

---

注意事项

1、关于long res = 0; res = int * int出现精度问题

原因：int * int 得到的值会转为int类型，哪怕乘积是一个long类型，所以我们这边应该先将乘数先转为一个long类型才可。

案例1：1237. 螺旋折线，在java中对于这种k参与运算并且相乘结果超int范围的，必须将其本身也设置为long类型。

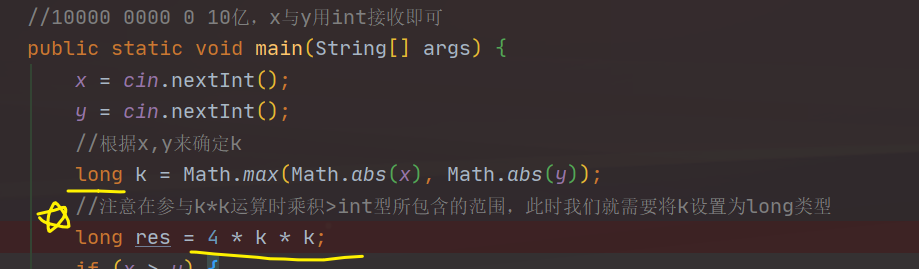
案例2：1814. 统计一个数组中好对子的数目

2、关于1e2问题

1e1就是10，若是有10个0，那么就是1e9情况。

---

技巧类

自定义Pair

自定义的键值对集合Pair：在acwing中需要自定义

static class Pair<K, V> {K x;V y;public Pair(K x, V y) {this.x = x;this.y = y;}
}

排序

①方式一：自定义类的话需要继承comparable接口，也就是实现compareTo方法

static class Node implements Comparable<Node> {public int ts;public int id;public Node(Integer ts, Integer id) {this.ts = ts;this.id = id;}public boolean equals(Node node) {return this.ts == node.ts && this.id == node.id;}@Overridepublic int compareTo(Node o) {if (this.ts == o.ts) return this.id - o.id;return this.ts - o.ts;}
}

②方式二：

//该接口是实现compare接口
Arrays.sort(list, (o1, o2)->{})

N维数组转一维

二维数组转一维：

int A, B;//A表示行数、B表示列数public int get(int i, int j) {return (i * B) + j;
}

三维数组转一维：

int A, B, C;public int get(int i, int j, int k) {return (i * B + j) * C + k;
}

位运算

与运算：

场景一：判断是偶数还是奇数
ch & 1 == 1 => 奇数     ch & 1 == 0  偶数

异或：

场景一：大写、小写字母转换，无需写if判断大小写来进行+32或-32，可直接进行ch ^= 1 << 5;  也就是异或32示例：https://leetcode.cn/problems/letter-case-permutation/
ch[i] ^= 1 << 5;//异或情况
a ^ b = c
a ^ c = b

状态压缩

5位状态：state = (1 << 5) - 1，此时即为11111

查看当前状态没有选择的：i = (1 << 5) - 1 - state

• 例如state=01100，最终i为10011。

当前状态补上新加的：state |= newState

• 例如state=00010，newState = 01100，最终结果为01110。

消除掉原先的一些状态：state = state & ~pack或者state ^ (state & pack)，两个等价

• 例如state = 11111，消除目标pack = 01100，最终结果为10011。

---

算法基础

枚举 √

指数型枚举

模板题链接：92. 递归实现指数型枚举

题目：从 1∼n这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

复杂度分析：时间复杂度O(2ⁿ)；空间复杂度O(n)

import java.util.*;class Main{private static int n;private static int[] arr;//0表示初始，1表示选，2表示不选public static void dfs(int u) {if (u == n) {//从选好的一组情况中来找到选的物品for (int i = 0; i < n; i++) {if (arr[i] == 1) {System.out.printf("%d ",i + 1);}}System.out.println();return;}//递归多种状态//选arr[u] = 1;dfs(u + 1);arr[u] = 0;//不选arr[u] = 2;dfs(u + 1);arr[u] = 0;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();arr = new int[n];dfs(0);}
}

---

排列型枚举

模板例题：94. 递归实现排列型枚举

示例：把 1∼n这n个整数排成一行后随机打乱顺序，输出所有可能的次序。

复杂度分析：时间复杂度为 O(n*n!)；空间复杂度为O(n)

class Main {static int N = 9;static int n;//存储结果集private static int[] state = new int[N];//存储该路径是否访问过private static int[] vis = new int[N];//递归处理//dfs(0)开始public static void dfs (int u) {if (u == n) {//输出对应的方案for (int i = 0; i < n; i ++) {System.out.printf("%d", state[i]);}System.out.println();return;}//遍历枚举多种情况for (int i = 0; i < n; i ++) {if (!visited[i]) {visited[i] = true;state[u] = i + 1;//真实的值//递归dfs(u + 1);//恢复visited[i] = false;state[u] = 0;}}}}

---

组合型枚举

模板题目：93. 递归实现组合型枚举

介绍：在排列型中进行升级，原本给定3个数让你找到所有3个排列方案，而在这里有n个数，让你找对应m个( <= n)个数组合的排列情况。

复杂度分析：时间复杂度O(mⁿ!)

class Main {static final int N = 15;static int n, m;//每个结果集都static int[] state = new int[N];public static void dfs(int u, int start) {//优化剪枝，提前结束if (u + (n - start) < m) return;//若是遍历的到终点个数个if (u == m) {//输出对应的方案for (int i = 0; i < n; i ++) {System.out.printf("%d ", state[i]);}System.out.println();}for (int i = start; i < n; i ++) {statue[u] = i + 1;dfs(u + 1, i + 1);statue[u] = 0;}}
}

---

模拟 √

日期天数问题：平年闰年情况

//平年28天，闰年为29天//判断闰年：不能被100整除,可以被4整除 或者  整除400
if (year % 100 != 0 && year % 4 == 0 || year % 400 == 0) static int[] months = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
//判断8位数是否是合法日期
public static boolean check(int d) {int year = d / 10000;int month = d % 10000 / 100;int day = d % 100;if (month > 12 || month == 0 || day > 31 || day == 0) return false;//闰年判断if (month != 2 && day > months[month]) return false;if (month == 2) {int leap = year % 4 == 0 && year % 100 != 0 || year % 400 == 0 ? 1 : 0;if (day > 28 + leap) return false;}return true;
}//判断日期的合法功能函数
public static boolean check(int year, int month, int day) {if (month > 12 || month == 0 || day > 31 || day == 0) return false;//闰年判断if (month != 2 && day > months[month]) return false;if (month == 2) {int leap = year % 4 == 0 && year % 100 != 0 || year % 400 == 0 ? 1 : 0;if (day > 28 + leap) return false;}return true;
}

日期时间点问题：

求 HH:mm:ss//获取到h小时m分钟s秒的总共秒数
public static int get_seconds(int h, int m, int s) {return h * 3600 + m * 60 + s;
} //将对应的总秒数去换算得到小时，分钟，秒数
int hour = time / 3600, minute = time % 3600 / 60, second = time % 60;

递归&分治 √

贪心 √

货仓选址-模板题

给你多个点，让你去确定在那个地点建仓库可以让来回距离最短：

将所有水平点存储到数组中对其进行排序，接着mid = (n + 1) / 2即可确定中间点，最后就是来进行求取距离。

• 若是有对应的公式推导成最终这个样子：|A₁ - B| + |A₂ - B| + |A₃ - B| … + |A_n - B|，那么最后就是ans += Math.abs(A[i] - A[mid])。

排序 √

归并排序

前缀和&差分 √

前缀和

一维前缀和：

s[i] = s[i - 1] + nums[i]
# 推导，其中nums的值需要从坐标1开始，若是默认给的从0开始则需要为s[i] = s[i - 1] + nums[i - 1]
s[1] = s[0] + nums[1]
s[2] = s[1] + nums[2] = nums[1] + nums[2]
s[3] = s[2] + nums[3] = nums[1] + nums[2] + nums[3]
# 计算范围：[1,3]   s[3] - s[1 - 1]   =>     [i, j]   s[i] - s[j - 1]

二维前缀和：

s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]# 计算范围 x1,y1   x2y2
sum = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]

差分（一维、二维、三维）

蓝桥杯三维差分题：AcWing 1232. 三体攻击

一维：

步骤一(反推b)：b[i] = a[i] - a[i - 1]中间步骤(范围操作)：
b[l] += c;
b[r + 1] -= c;步骤三：a[i] = a[i - 1] + b[i]

二维：

步骤一(反推b)：b[i][j] = a[i][j] + a[i - 1][j - 1] - a[i - 1][j] - a[i][j - 1]中间步骤(范围操作)：
b[x1][y1] += c
b[x2 + 1][y1] -= c
b[x1][y2 + 1] -= c
b[x2 + 1][y2 + 1] += c步骤三(反推a)：a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j]

三维：

//步骤一：首先确定三维前缀和公式
b(x, y, z) = a(x, y, z) - a(x - 1, y, z) - a(x, y - 1, z) + a(x - 1, y - 1, z)- a(x, y, z - 1) + a(x - 1, y, z - 1) + a(x, y - 1, z - 1) - a(x - 1, y - 1, z - 1)中间步骤(范围操作)：
二维正面（以z1为）
b[x1    ][y1    ][z1] += val
b[x1    ][y2 + 1][z1] -= val
b[x2 + 1][y1    ][z1] -= val
b[x2 + 1][y2 + 1][z1] += val
转为z2+1，且符号改变
b[x1    ][y1    ][z2 + 1] -= val
b[x1    ][y2 + 1][z2 + 1] += val
b[x2 + 1][y1    ][z2 + 1] += val
b[x2 + 1][y2 + 1][z2 + 1] -= val步骤三：最后反推求出a数组推导来进行计算
a(x, y, z) = b(x, y, z) + a(x - 1, y, z) + a(x, y - 1, z) - a(x - 1, y - 1, z)+ a(x, y, z - 1) - a(x - 1, y, z - 1) - a(x, y - 1, z - 1) + a(x - 1, y - 1, z - 1) 

扩展：

1、前缀异或

相关题目：

• 第 314 场周赛—6201. 找出前缀异或的原始数组

二分 √

规律：一组单调递增或者递减情况(不限制于数字)情况时可以采用二分来进行优化。【O(n) -> O(logn)】

模板：

//第一类二分写法：check
int l = 0, r = n;
while (l < r) {int mid = l + r >> 1;if (mid >= target) l = mid + 1;else r = mid;
}int l = 0, r = n;
while (l < r) {int mid = (l + r + 1) >> 1;if (nums2[i] >= nums1[mid]) l = mid - 1;else r = mid;
}//第二种二分写法：
while (l != r) {int mid = l + ((r - l) >> 1);if (nums1[mid] < nums2[i]) l = mid + 1;else r = mid;
}

题单

蓝桥杯13届真题-求阶乘（算数基本定理、二分）

搜索

DFS √

题型：最大长度

模板：

void dfs(int step)    //步长
{if(/*跳出循环的条件*/){return;    //return十分关键，否则循环将会无法跳出}/*函数主体对功能进行实现*/for(/*对现有条件进行罗列*/){if(/*判断是否合理*/){//将条件修改dfs(/*新的step*/)/*！重中之重，当跳出那层循环后将数据全部归位*/}    }
}

矩阵模板：

int f[4][2]={{0,1},{0,-1},{1,0},{-1,0}};    //用于判断下一步怎么走向几个方向走就是几个数据
void dfs(int x,int y){        //进入点的坐标if(/*跳出循环的条件*/){/*作出相应操作*/return;        //不要忘了return}for(int i=0;i</*f的长度*/;i++){int x0=x+f[i][0];    /*此处是更新点的坐标，注意是直接让原来的点加上这个数据，不是直接等于*/int y0=y+f[i][1];if(/*用新坐标x0,y0判断是否符合条件*/){dfs(x0,y0);    //用新的坐标进行递归}}
}

BFS √

题单

3、蓝桥杯13届真题-回忆迷宫（模拟、BFS）

模板

题型：最短路径。

模板：

1、二叉树：

class Solution {public static void main (String[] args) {Queue<TreeNode> queue = new LinkedList<>();queue.offer(xx);//添加root节点while (!queue.isEmpty()) {int size = queue.size();for (int i = 0; i < size; i++) {//取出node结点进行操作TreeNode node = queue.poll();//放置左右子节点if (node.left != null) queue.offer(node.left);if (node.right != null) queue.offer(node.right);}res.add(1.0 * sum / size);}}
}

2、二维矩阵：

class Point {private int x;private int y;public Point(int x, int y) {this.x = x;this.y = y;}
}class Solution {public static void main (String[] args) {Queue<Point> queue = new LinkedList<>();queue.offer(new Point(1,2));//出发点while (!queue.isEmpty()) {int size = queue.size();for (int i = 0; i < size; i++) {//取出Point结点进行操作Point point = queue.poll();//进行操作//放置四个方向的节点for (int d = 0; d < dicts.length; d++) {int x = point.x + dicts[d][0];int y = point.y + dicts[d][1];queue.offer(new Point(x, y))}}}}
}

3、坐标点写法：

class Solution {static final int N = 110;static int[] q = new int[N * N];static int hh, tt;//hh表示头指针(用于出队)，tt表示入队指针//四个方向  (0, 1) (0, -1) (1, 0) (-1, 0)static int[] dx = {0, 0, 1, -1};static int[] dy = {1, -1, 0, 0};//矩阵static int[][] g = new int[N][N];static int H, W;//将二维坐标转为一个数字public static int get(int x, int y) {return x * (W + 1) + y;}public static void main (String[] args) {//bfs过程while (hh < tt) {int top = q[hh ++];int x = top / (W + 1);int y = top % (W + 1);//四个方向for (int k = 0; k < 4; k ++) {int xx = x + dx[k];int yy = y + dy[k];//搜索校验（边界情况 && 其他情况xxx）if (xx >= 1 && yy >= 1 && xx <= H && yy <= W) {//入队q[tt ++] = get(x, y);//相关动作xxx}}}}
}

IDA*

回溯

字符串

KMP算法

模板：

package com.changlu.string;public class KMP {public static void main(String[] args) {//APISystem.out.println("ababcabcaabbcdeabcdef".indexOf("abcaabb"));//手写System.out.println(kmp("ababcabcaabbcdeabcdef", "abcaabb"));}public static int kmp (String str, String sub) {int[] next = getNext(sub);for (int i = 0, j = 0; i < str.length(); i++) {while (j > 0 && str.charAt(i) != sub.charAt(j)) {j = next[j - 1];}if (str.charAt(i) == sub.charAt(j)) j++;//若是匹配到最后if (j == sub.length()) {return i - j + 1;}}return -1;}public static int[] getNext(String str) {int[] next = new int[str.length()];next[0] = 0;for (int i = 1, j = 0; i < str.length(); i ++) {while (j > 0 && str.charAt(i) != str.charAt(j)) {j = next[j - 1];}//若是当前字符相等if (str.charAt(i) == str.charAt(j)) {j++;}next[i] = j;}return next;}}

动态规划 √

线性DP

背包DP

区间DP

树形DP

状态压缩DP

计数DP

数学 √

数论

算法基本定理

知识点

算数基本定理

题单

蓝桥杯13届真题-求阶乘（算数基本定理、二分）

约数

约数个数及约数之和知识点(含公式)

最大公约数与公倍数

//最大公约数 greatest common divisor
int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);
}
//最小公倍数  Lowest Common Multiple
int lcm(int a, int b) {return a * b / gcd(a, b);
}

欧拉筛法（含朴素筛法、埃式筛法）

数论之欧拉筛法（含朴素筛选、埃式筛选详细代码）

质数-欧拉筛

模板：

//欧拉筛所需要数组
//flag表示合数数组，true为合数
static boolean[] flag = new boolean[N];
//存储质数
static int[] primes = new int[N];
static int cnt = 0;//欧拉筛
public static void getPrimes(int n) {//遍历所有情况for (int i = 2; i <= n; i++) {if (!flag[i]) primes[cnt++] = i;//枚举所有primes数组中的情况来提前构造合数for (int j = 0; j < cnt && primes[j] * i <= n; j ++) {int pre = primes[j] * i;flag[pre] = true;if (i % primes[j] == 0) break;}}
}//判断是否是质数（由于之前primes数组仅仅开了sqrt(20亿)也就只有50万，所以这里需要进行遍历一遍质数数组来进行判断校验）
public static boolean isPrime(int x) {//若是x在50万范围，直接从flag数组中判断返回即可if (x < N) return !flag[x];//若是>=50万，那么就进行遍历质数数组看是否有能够整除的，如果有那么直接返回for (int i = 0; primes[i] <= x / primes[i]; i++) {if (x % primes[i] == 0) return false;}return true;
}

欧几里得与扩展欧几里得

欧几里得与扩展欧几里得算法(含推导过程及代码)

辗转相除（含辗转相减法）

辗转相除以及辗转相减法

组合数学

容斥定理

容斥定理：能被 a 或 b 整除的数的个数 = 能够被 a 整除的数的个数 + 能够被 b 整除的数的个数 - 既能被 a 又能被 b 整除的数的个数。

题单

leetcode、878. 第 N 个神奇数字(困难)

快速幂

快速幂及矩阵快速幂分析及代码实现

模板：

private static final long MOD = 1000000007;/*** 递归快速幂* @param a 实数a* @param n 阶数n，三种情况，n=0,n=奇数，n=偶数* @return*/
public static long qpow(long a, long n){if (n == 0){return 1;}else if ((n & 1) == 1) {  //奇数return qpow(a, n -1) * a % MOD;}else {long temp = qpow(a, n / 2) % MOD;return temp * temp % MOD;}
}/*** 非递归方式*/
public static long qpow2(long a, long n) {long ans = 1;while ( n != 0) {if ((n & 1) == 1) { //若是n为奇数ans *= a % MOD;ans %= MOD;//求模处理}a *= a % MOD; //这个就表示偶数情况a = a % MOD;//求模处理n = n >> 1;}return ans;
}

矩阵

数据结构

哈希表 √

树状数组 √

并查集

线段树 √

#图论 √

树上问题

树的直径

计算机几何

杂项

双指针 √