※5.1.4.4.1

5.1二叉树

class Node<V>{
V value;
Node left;
Node right;
}

用递归和非递归两种方式实现二叉树的先序、中序、后序遍历
如何直观的打印一颗二叉树
如何完成二叉树的宽度优先遍历（常见题目：求一颗二叉树的宽度）

5.1.1例1：用递归和非递归两种方式实现二叉树的先序、中序、后序遍历

递归序是通过递归方法生成的序列，而非递归序则是通过循环和栈的辅助实现的序列。两者在序列化顺序上是一致的，都是按照 “根结点、左子树、右子树” 的顺序遍历二叉树。

5.1.1.1递归序的先序、中序、后序遍历

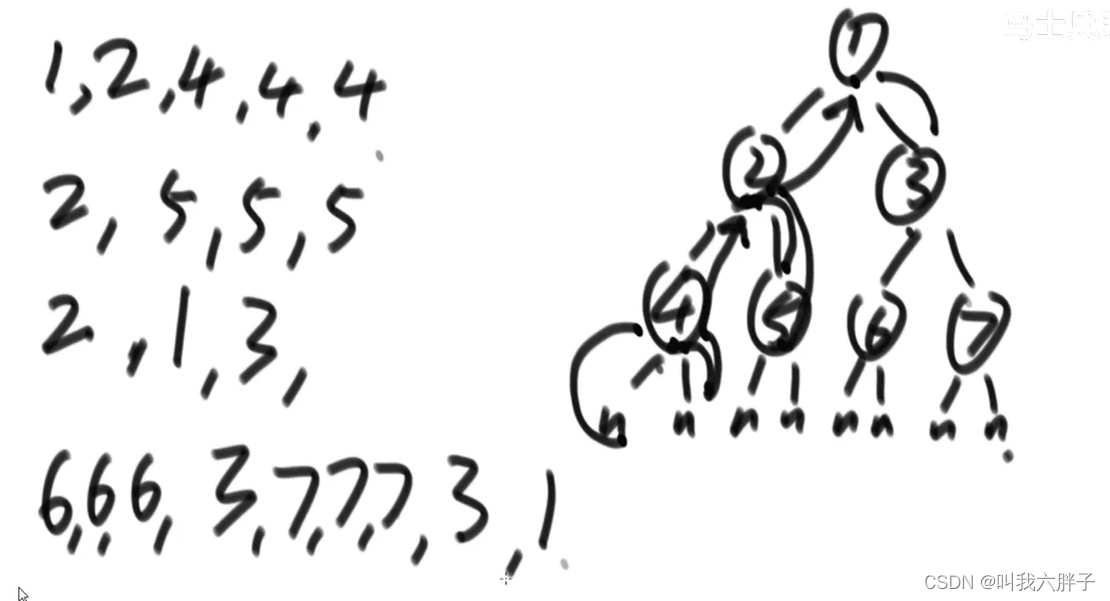
先序遍历：

头左右
对于所有子树来说，先打印头节点，再打印左子树上的所有节点，再打印右树上的所有节点（对于每一个子树都是先打印左，后打印右）
1，2，4，5，3，6，7
第一次碰到的就打印，不是就不打印

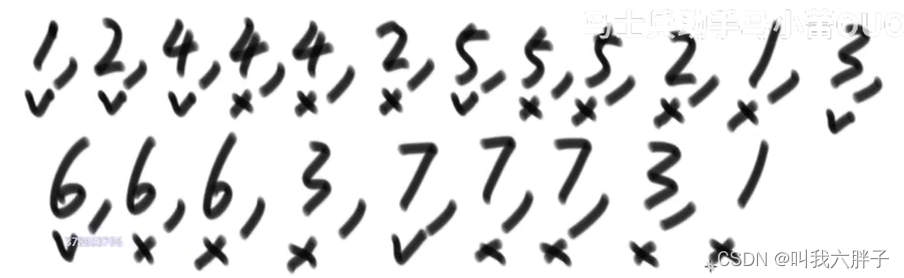
中序遍历：

左头右
先打印左树，再打印头，再打印右树
4，2，5，1，6，3，7
利用递归序，第二次再打印，不是第二次什么也不做

后序遍历：

左右头
先打印左树，再打印右树，再打印头
4，5，2，6，7，3，1
利用递归序，第三次再打印，不是第三次什么也不做

#include <iostream>using namespace std;// 定义二叉树的结点
struct Node {int data;Node* left;Node* right;
};// 创建一个新的二叉树结点
Node* createNode(int data) {Node* newNode = new Node();if (newNode == nullptr) {cout << "内存分配失败!" << endl;return nullptr;}newNode->data = data;newNode->left = nullptr;newNode->right = nullptr;return newNode;
}// 先序遍历
void preorderTraversal(Node* root) {if (root == nullptr)return;cout << root->data << " ";preorderTraversal(root->left);preorderTraversal(root->right);
}// 中序遍历
void inorderTraversal(Node* root) {if (root == nullptr)return;inorderTraversal(root->left);cout << root->data << " ";inorderTraversal(root->right);
}// 后序遍历
void postorderTraversal(Node* root) {if (root == nullptr)return;postorderTraversal(root->left);postorderTraversal(root->right);cout << root->data << " ";
}int main() {// 创建二叉树Node* root = createNode(1);root->left = createNode(2);root->right = createNode(3);root->left->left = createNode(4);root->left->right = createNode(5);root->right->left = createNode(6);root->right->right = createNode(7);// 输出先序遍历cout << "先序遍历结果：" << endl;preorderTraversal(root);cout << endl;// 输出中序遍历cout << "中序遍历结果：" << endl;inorderTraversal(root);cout << endl;// 输出后序遍历cout << "后序遍历结果：" << endl;postorderTraversal(root);cout << endl;return 0;
}

5.1.1.2非递归序的先序、中序、后序遍历

先序遍历：

头左右
1，2，4，5，3，6，7
每次把头节点放入栈里，从栈中弹出一个节点cur，打印（处理）cur，先右边放入栈中，再左边放入栈中，从头（从栈中弹出一个节点cur）开始周而复始
先放头1节点，弹出1打印
放入右节点3，放入左节点2，弹出2打印
先放入5节点，再放入4节点，弹出4打印，
先放右再放左，都没有所以什么也不做，弹出5打印
先放右再放左，都没有所以什么也不做，弹出3打印
先放右节点7，再放左节点6，弹出6打印
先放右再放左，都没有所以什么也不做，弹出7打印

中序遍历：

左头右
每棵树左边界进栈，依次弹出节点的过程中打印，对弹出节点的右树循环周而复始
1，2，4进栈
弹出4打印4，没有右树
弹出2，打印2，有右树5，压栈5
弹出5，打印5，没有右树
弹出1，打印1，有右树，压栈3，6
弹出6，打印6，没有右树
弹出3，打印3，有右树，压栈7
弹出7，打印7
4，2，5，1，6，3，7

放入栈的顺序是从头到左，弹出栈的顺序是左头，之后取右树再次先左再头……

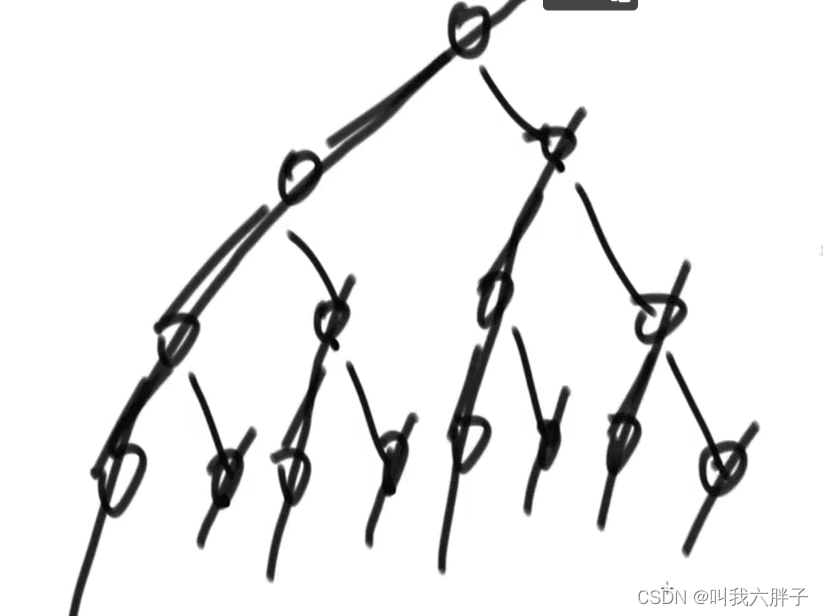
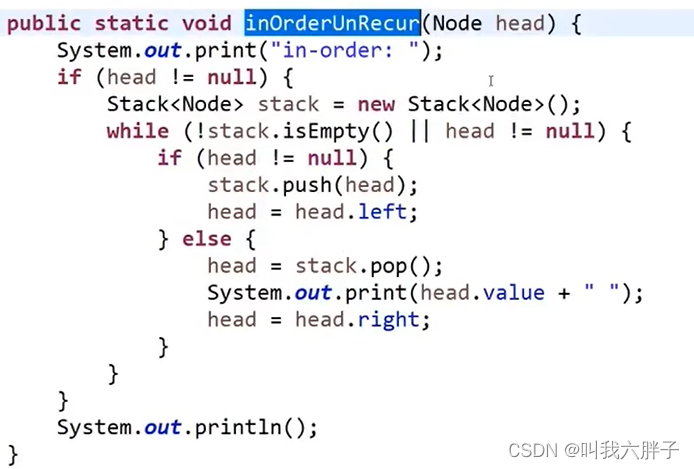
后序遍历：

左右头
放入到栈中是头右左，
从收栈弹出反转变成了左右头
4，5，2，6，7，3，1

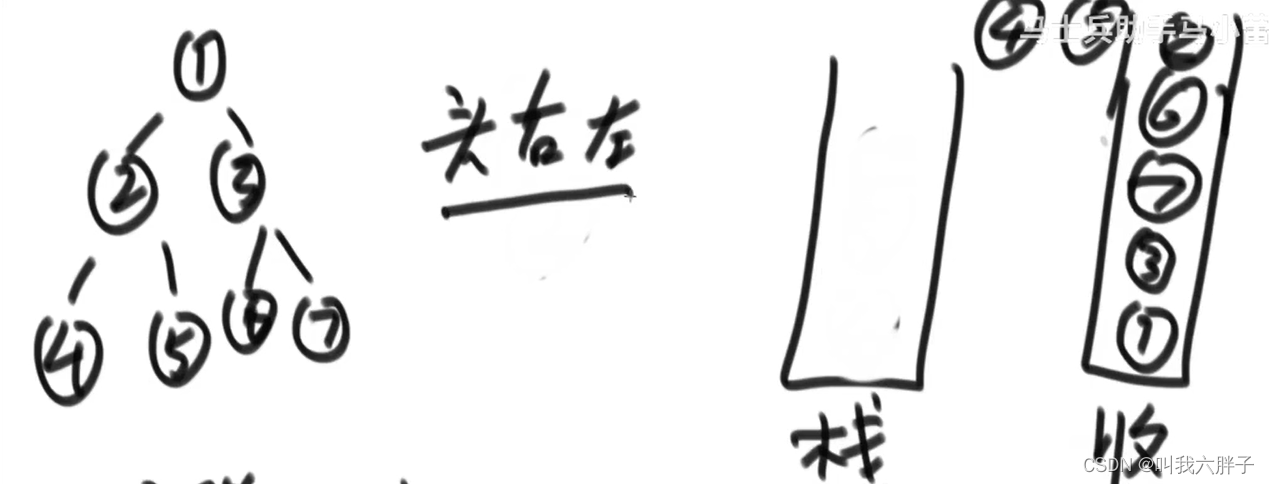
弹，cur
cur放入收栈
先左再右
循环

先压栈头1节点，弹出1节点压栈到收栈
压栈2，压栈3，弹出3，3压栈到收栈
压栈6，压栈7，弹出7，7压栈到收栈
压栈左右为空，弹出6，6压栈到收栈
压栈左右为空，弹出2，2压栈到收栈
压栈4，压栈5，弹出5，5压栈到收栈
压栈左右为空，弹出4，4压栈到收栈

弹出收栈4，5，2，6，7，3，1

#include <iostream>
#include <stack>using namespace std;// 定义二叉树的结点
struct Node {int data;Node* left;Node* right;
};// 创建一个新的二叉树结点
Node* createNode(int data) {Node* newNode = new Node();if (newNode == nullptr) {cout << "内存分配失败!" << endl;return nullptr;}newNode->data = data;newNode->left = nullptr;newNode->right = nullptr;return newNode;
}// 非递归先序遍历
void iterativePreorderTraversal(Node* root) {if (root == nullptr)return;stack<Node*> st;st.push(root);while (!st.empty()) {Node* curr = st.top();st.pop();cout << curr->data << " ";if (curr->right)st.push(curr->right);if (curr->left)st.push(curr->left);}
}// 非递归中序遍历
void iterativeInorderTraversal(Node* root) {if (root == nullptr)return;stack<Node*> st;Node* curr = root;while (curr != nullptr || !st.empty()) {while (curr != nullptr) {st.push(curr);curr = curr->left;}curr = st.top();st.pop();cout << curr->data << " ";curr = curr->right;}
}// 非递归后序遍历
void iterativePostorderTraversal(Node* root) {if (root == nullptr)return;stack<Node*> st1, st2;st1.push(root);while (!st1.empty()) {Node* curr = st1.top();st1.pop();st2.push(curr);if (curr->left)st1.push(curr->left);if (curr->right)st1.push(curr->right);}while (!st2.empty()) {Node* curr = st2.top();st2.pop();cout << curr->data << " ";}
}int main() {// 创建二叉树Node* root = createNode(1);root->left = createNode(2);root->right = createNode(3);root->left->left = createNode(4);root->left->right = createNode(5);root->right->left = createNode(6);root->right->right = createNode(7);// 输出非递归先序遍历cout << "非递归先序遍历结果：" << endl;iterativePreorderTraversal(root);cout << endl;// 输出非递归中序遍历cout << "非递归中序遍历结果：" << endl;iterativeInorderTraversal(root);cout << endl;// 输出非递归后序遍历cout << "非递归后序遍历结果：" << endl;iterativePostorderTraversal(root);cout << endl;return 0;
}

5.1.2例2：如何直观的打印一颗二叉树

如第三个树

5.1.3例3：如何完成二叉树的宽度优先遍历

先序遍历就是深度优先遍历

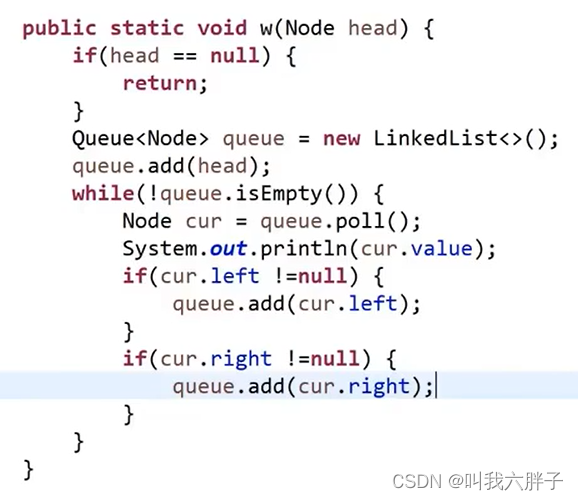
宽度遍历用队列（广度优先遍历），头进尾出（先进先出）弹出就打印

广度优先遍历代码

#include <iostream>
#include <queue>using namespace std;struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 宽度优先搜索遍历函数
void BFS(TreeNode* root) {if (root == nullptr) return;queue<TreeNode*> q;q.push(root);while (!q.empty()) {TreeNode* node = q.front();q.pop();cout << node->val << " ";  // 打印出队节点的值if (node->left) {q.push(node->left);}if (node->right) {q.push(node->right);}}
}int main() {// 构建二叉树TreeNode* root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);root->left->left = new TreeNode(4);root->left->right = new TreeNode(5);root->right->left = new TreeNode(6);root->right->right = new TreeNode(7);cout << "BFS traversal: ";BFS(root);return 0;
}

深度优先遍历代码

void DFS(TreeNode* node) {if (node == nullptr)return;cout << node->val << " ";  // 打印当前节点的值DFS(node->left);  // 递归遍历左子树DFS(node->right);  // 递归遍历右子树
}

5.1.3.1求一颗二叉树的宽度

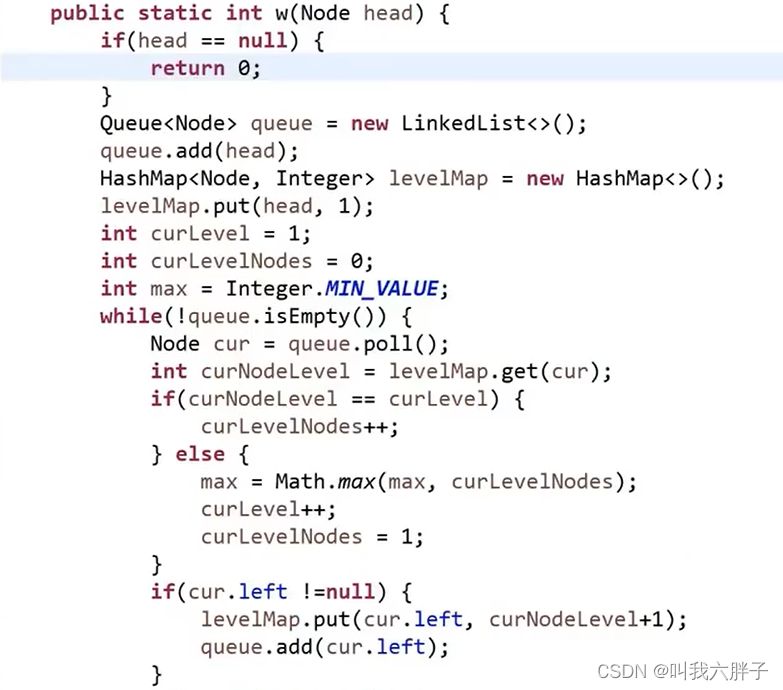
5.1.3.1.1方法1队列哈希表方法

需要知道哪一层的节点个数，准备一张表，记录任何一个点在第几层

当前在哪一层 curLevel
当前层发现几个节点 curLevelNodes
所有层中那一层节点数最多 max

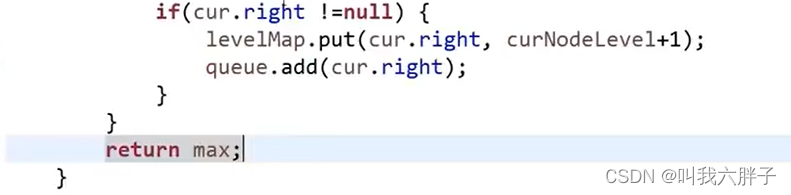
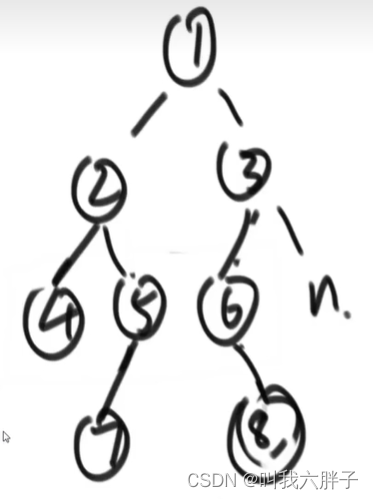
5.1.3.1.2方法2队列方法

NodeCurend=1
Nodenextend=null
int Curlevel=0

让1节点进队列
弹出1节点先让左孩子进栈，看Nodenextend是否为空，如果为空，把Nodenextend设置为进栈的节点2
再让右孩子3进栈，Nodenextend=3，int Curlevel=1
当前节点是不是当前层最后一个节点，是max=1，让NodeCurend拷贝Nodenextend，NodeCurend=3，使Nodenextend=null，让int Curlevel=0

弹出2节点，让2节点的左孩子进栈，再让右孩子4进栈，但是左孩子是nullptr，，所以4进栈，int Curlevel=1
弹出3节点，让3节点的左孩子5进栈，再让右孩子6进栈，Nodenextend=6（当前层谁最后进栈谁是Nodenextend），int Curlevel=2，当前层后面不会进了max=2，NodeCurend拷贝Nodenextend，NodeCurend=6，使Nodenextend=null，让int Curlevel=0

弹出4节点，让4节点的左孩子进栈，再让右孩子进栈，但是左右孩子都是nullptr，int Curlevel=1
弹出5节点，让5节点的左孩子7进栈，再让右孩子进栈，但是右孩子是nullptr，Nodenextend=7，int Curlevel=2
弹出6节点，让6节点的左孩子进栈，再让右孩子8进栈，但是左孩子是nullptr，Nodenextend=8，int Curlevel=3，6节点为本层的结束max=3，NodeCurend拷贝Nodenextend，NodeCurend=8，使Nodenextend=null，让int Curlevel=0

……

5.1.4例4：二叉树的相关概念及其实现判断

5.1.4.1判断一颗二叉树是否是搜索二叉树（BST）？

搜索二叉树（Binary Search Tree，简称BST）是一种具有特殊性质的二叉树。它满足以下定义：

每个节点都包含一个键（key）和一个相关联的值（value）。
对于任意节点，其左子树中的所有键的值都小于该节点的键的值。
对于任意节点，其右子树中的所有键的值都大于该节点的键的值。
左子树和右子树都是搜索二叉树。
也就是说，对于搜索二叉树中的任意节点，其左子树中的所有节点的键都小于该节点的键，而右子树中的所有节点的键都大于该节点的键。这个特点使得搜索二叉树有很好的查找和排序性能，在许多应用中被广泛使用。

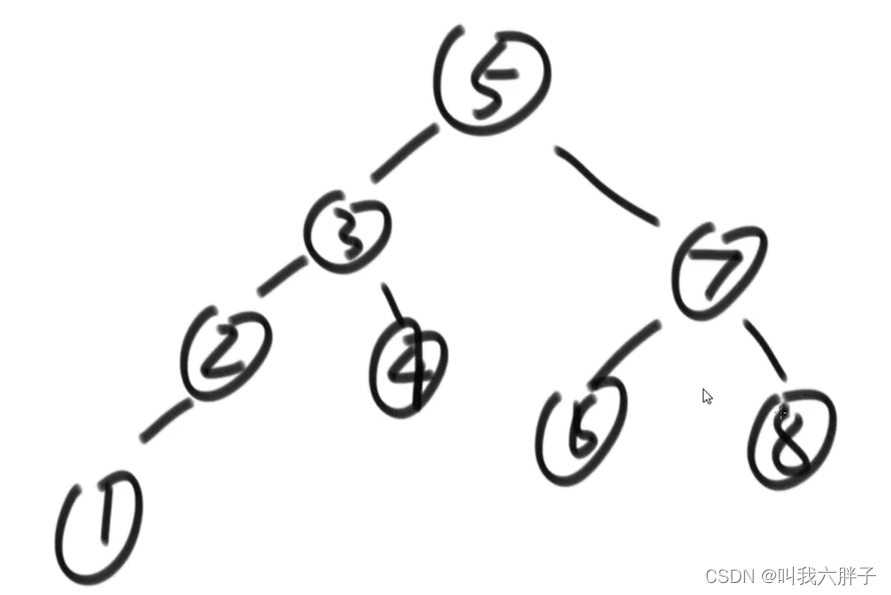
中序遍历

使用中序遍历，如果输出结果一直在升序，那它一定是搜索二叉树

#include <limits>
int preValue = std::numeric_limits<int>::min();bool checkBST(Node* head)
{if (head == nullptr){return true;}bool isLeftBST = checkBST(head->left);if (!isLeftBST)//发现左树不是搜索二叉树就直接返回false{return false;}if (head->data <= preValue)//和上次搜索到值相比较，小于等于就返回false{return false;}else//大于就使preValue等于当前值，下次循环就可以判断了{preValue = head->data;}return checkBST(head->right);
}

次一点的方法

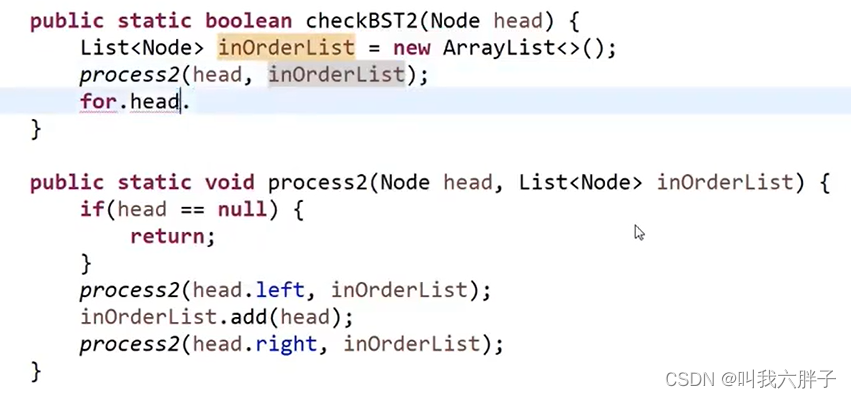
非递归方式

5.1.4.2判断二叉树是否是完全二叉树（CBT）？

完全二叉树（Complete Binary Tree）是一种特殊的二叉树结构（除了最后一层都是满的，最后一层即便不满，也是从左到右依次满的）

（1）任一节点，一旦有右无左直接输出false
（2）在（1）不违规条件下，如果遇到左右两个孩子不双全的情况，接下来遇到的所有节点都必须是叶节点

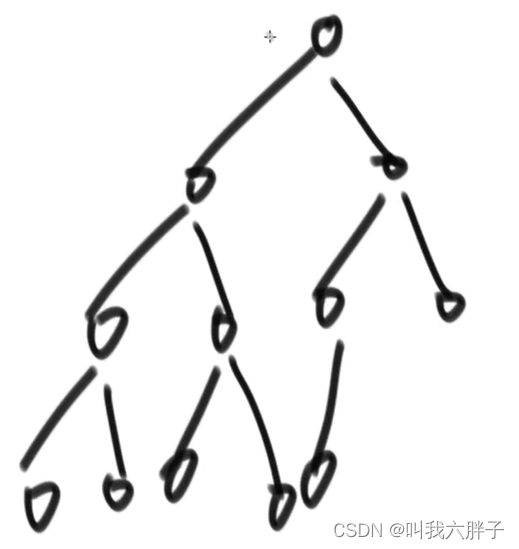
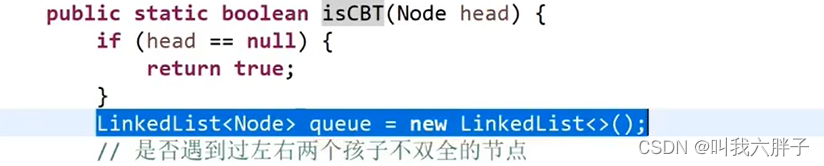
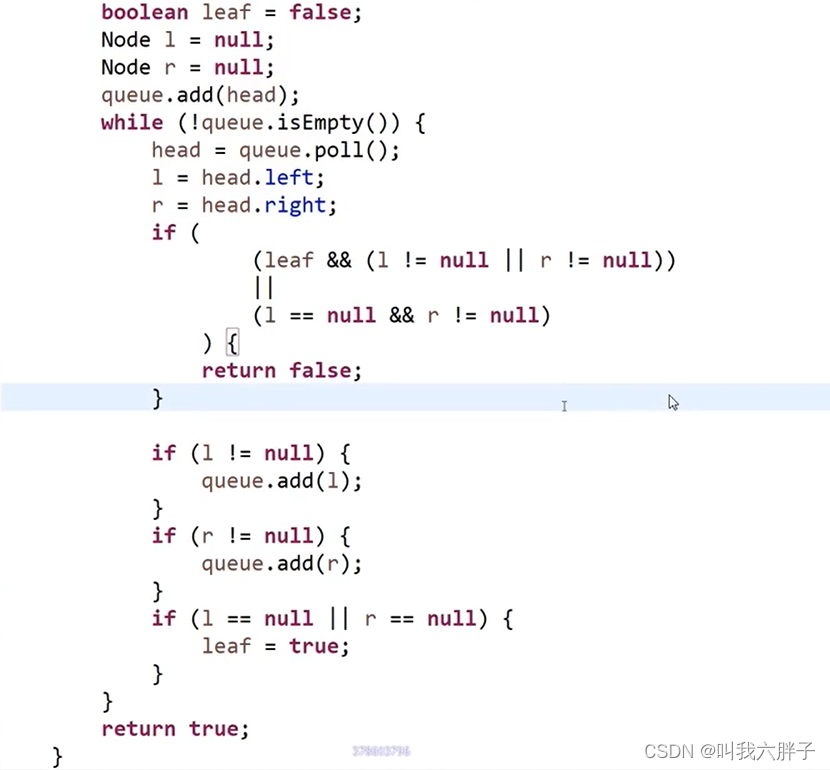
5.1.4.3判断一颗二叉树是否是满二叉树？

麻烦做法：
先求二叉树最大深度L，再求二叉树节点个数N
最大深度L和节点个数N满足:N=2^L-1
如果满足此关系必定是满二叉树，如果是满二叉树必定满足此关系

5.1.4.4判断一棵二叉树是否是平衡二叉树？

平衡二叉树：对于任一子树来说，左树和右树的高度差不超过1

※5.1.4.5判断是搜索二叉树、满二叉树、平衡二叉树的递归套路（可以解决一切树形DP问题）

树形DP问题是面试题内最难的二叉树类型的问题了
都是基于怎么向左树要信息，怎么向右树要信息

※判断是否是平衡二叉树？

左树需要返回是否平衡，高度是多少，右树也相同

#include<cmath>
class ReturnType
{
public:bool isBalanced;int height;ReturnType(bool isB, int hei)//构造函数{isBalanced = isB;height = hei;}
};ReturnType* process(Node* x)
{if (!x) return new ReturnType(true, 0);//x为空的时候返回哪两个值（是否是平衡树true，高度0）ReturnType leftData = *process(x->left);ReturnType rightData = *process(x->right);int height = max(leftData.height, rightData.height) + 1;//左树和右树高度较大的一个加1bool isBalanced = leftData.isBalanced && rightData.isBalanced && abs(leftData.height - rightData.height) < 2;//左树是平衡树，右树是平衡树，左树和右树的差的绝对值小于2ReturnType* ans = new ReturnType(isBalanced, height);//最后返回的值（以x为头的是否是平衡二叉树，高度）return ans;
}bool isBalanced(Node* head)
{return process(head)->isBalanced;
}

※判断是否是搜索二叉树？

需要左树是搜索二叉树，左树最大值max
需要右树是搜索二叉树，右树最小值min
左树最大值max < x（头节点）
右树最小值min > x（头节点）
现在需求不一样，但是必须每一个节点的需求是一样的才是递归

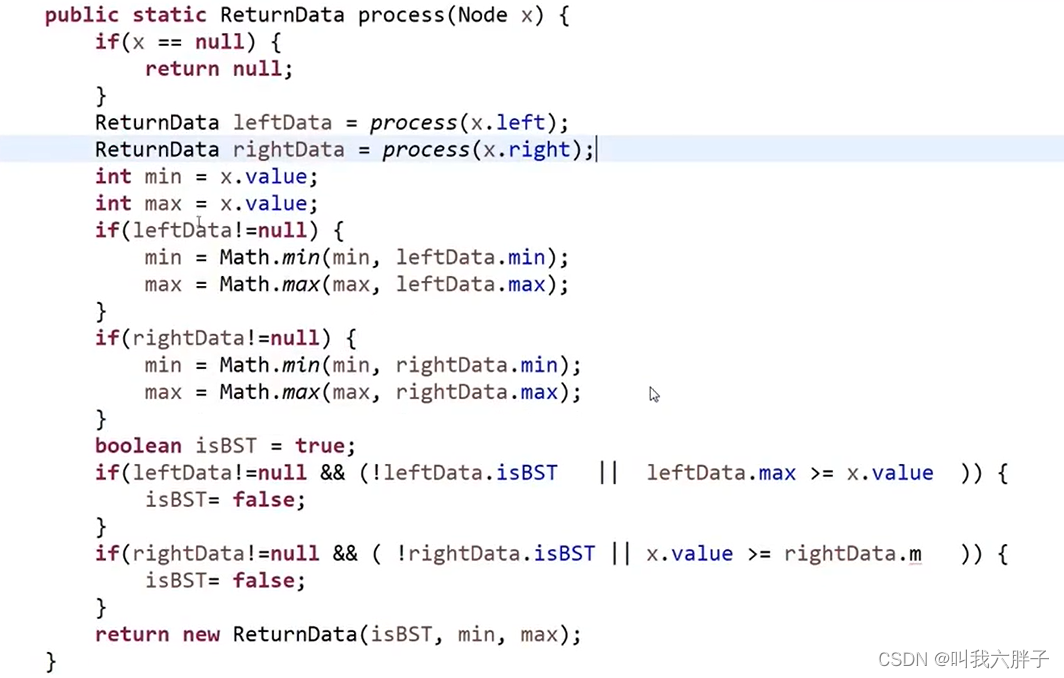
//是否是搜索二叉树？
class ReturnData
{
public:bool isBST;//根据需求要三个信息int min;int max;ReturnData(bool is,int mi,int ma)//构造函数{isBST = is;min = mi;max = ma;}
};
ReturnData* process(Node* x)
{if (!x)return nullptr;ReturnData* leftData = process(x->left);//默认左树给我一个信息ReturnData* rightData = process(x->right);//默认右树给我一个信息int Min = x->data;int Max = x->data;if (leftData!=nullptr)//如果左边得到的信息不为空，则有东西{Min = std::min(Min, leftData->min);//如果左树不为空，则左树值和x（或当前值）比大小，取最小值，找到左树最小值Max = std::max(Max, leftData->max);//如果左树不为空，则左树值和x（或当前值）比大小，取最大值，找到左树最大值}if (rightData != nullptr){Min = std::min(Min, rightData->min);//如果右树不为空，则左树值和x（或当前值）比大小，取最小值，找到右树最小值Max = std::max(Max, rightData->max);//如果右树不为空，则左树值和x（或当前值）比大小，取最大值，找到右树最大值}bool isBST = true;//整棵树书否是搜索二叉树，默认是//左边不是搜索二叉树了，返回false。左边最大值大于x了，返回falseif (leftData != nullptr && (!leftData->isBST || leftData->max >= x->data)){isBST = false;}//右边不是搜索二叉树了，返回false。右边最小值小于x了，返回falseif (rightData != nullptr && (!rightData->isBST || x->data >= rightData->min)){isBST = false;}return new ReturnData(isBST, Min, Max);//需求给了三个信息，返回三个值
}
bool isBST(Node* x)
{return process(x)->isBST;
}

※判断是否是满二叉树？

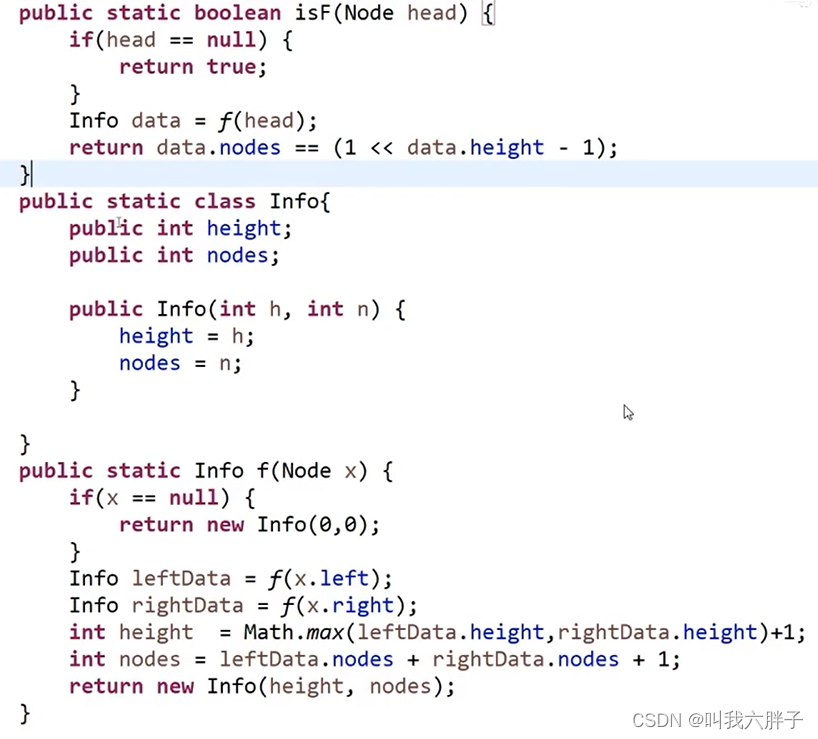
需知整棵树高度和节点个数

//是否是满二叉树？
class Info
{
public:int height;int nodes;Info(int h,int n){height = h;nodes = n;}
};Info* process(Node* x)
{if (!x)return new Info(0, 0);Info* leftData = process(x->left);Info* rightData = process(x->right);int height = max(leftData->height, rightData->height) + 1;int nodes = leftData->nodes + rightData->nodes + 1;return new Info(height, nodes);
};bool isF(Node* head){if (!head)return true;Info* data = process(head);return data->nodes == (1 << data->height - 1);//相当于2^L-1}

5.1.5例5：最低公共祖先节点

给定两个二叉树的节点node1和node2找到他们的最低公共祖先节点

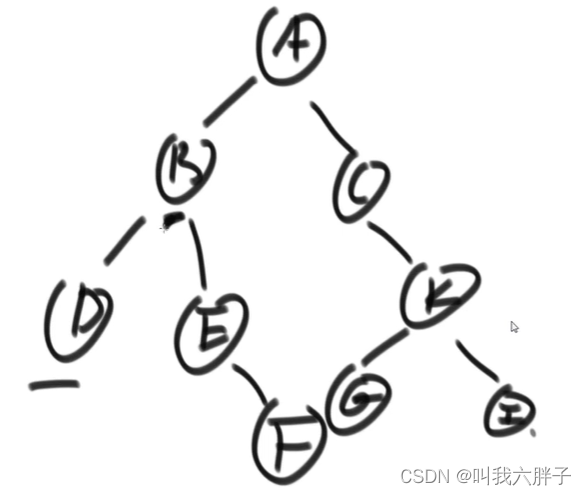
往上走，哪一个点是最初汇聚的点，第一个汇聚的点就是最低公共祖先

如E和F的最低公共祖先为E
如D和I的最低公共祖先为A

5.1.5.1方法1

往上遍历过程生成一个链，用容器记录链，在另一节点向上遍历时走到容器记录过的节点即为最低公共祖先
需要二叉树头，两个节点

#include<iostream>
#include<map>
#include<set>
#include <unordered_map>using namespace std;struct Node {int value;Node* left;Node* right;Node(int x) : value(x), left(nullptr), right(nullptr) {}
};void process(Node* head, map<Node*, Node*>* fatherMap) {if (!head) return;fatherMap->insert(make_pair(head->left, head));fatherMap->insert(make_pair(head->right, head));process(head->left, fatherMap);//记录左儿子和父节点process(head->right, fatherMap);//记录右儿子和父节点
}//o1和o2一定属于head为头的树
//返回o1和o2的最低公共祖先
Node* lca(Node* head, Node* o1, Node* o2) {auto* fatherMap = new map<Node*, Node*>();fatherMap->insert(make_pair(head, head));//设置head的父节点自己process(head, fatherMap);auto* set1 = new set<Node*>();//记录下o1往上整条链的节点set1->insert(o1);//先放入o1Node* cur = o1;//当前节点来到o1位置//o1经过的节点都放入set1中while (cur != fatherMap->find(cur)->second) {set1->insert(cur);cur = fatherMap->find(cur)->second;}set1->insert(head);cur = o2;//o2经过的节点都放入set1中，并且每经过一个点，都看在不在set中while (cur != fatherMap->find(cur)->second) {if (set1->find(cur) != set1->end())return cur;else {cur = fatherMap->find(cur)->second;}}return head;
}int main() {Node* head = new Node(8);head->left = new Node(6);head->right = new Node(10);head->left->left = new Node(4);Node* o1 = head->left->right = new Node(7);Node* o2 = head->left->left->left = new Node(1);head->left->left->right = new Node(5);head->right->left = new Node(9);head->right->right = new Node(11);cout << lca(head, o1, o2)->value << endl;
}

5.1.5.2方法2

情况1：o1是o2的最低公共祖先（LCA），或o2是o1的最低公共祖先
情况2：o1和o2不互为最低公共祖先（LCA）

Node* lowestAncestor(Node* head, Node* o1, Node* o2)
{if (head == nullptr || head == o1 || head == o2){return head;}Node* left = lowestAncestor(head->left, o1, o2);Node* right = lowestAncestor(head->right, o1, o2);if (left != nullptr && right != nullptr)//左树右树上都不为空就返回头部{return head;}return left != nullptr ? left : right;//两颗树并不都有返回值，谁不为空返回谁
}

在一个4层的完全二叉树中，o1，o2都在右树中，代码会怎么在左树中运行的状况

在一个4层的完全二叉树中，o1和o2都在右树中，那么代码将按照以下方式在左树中运行：

运行到第1行，此时head参数指向根节点。

运行到第3行，由于head不为空且不等于o1和o2，不会进入if语句，继续执行下一行。

运行到第7行，递归调用lowestAncestor函数传入head->left，即根节点的左子节点，在左树中进行递归。

递归调用的时候，继续从第1行开始执行，将左子节点作为新的head参数。

运行到第3行，由于head不为空且不等于o1和o2，不会进入if语句，继续执行下一行。

运行到第7行，继续递归调用lowestAncestor函数传入head->left，即左子节点的左子节点，在左树中继续递归。

重复步骤4-6，直到递归到最底层的叶子节点。

当递归到最底层叶子节点时，head为nullptr，因此第5行的条件判断为true，返回nullptr。

返回到上一层递归调用处，继续执行第6行。

运行到第6行，递归调用lowestAncestor函数传入head->right，即左子节点的右子节点，在左树中继续递归。

重复步骤4-10，直到递归到包含o1和o2的子树。

当递归到包含o1和o2的子树时，第3行的条件判断为true，返回包含o1和o2的子树的根节点。

因此，在这种情况下，代码将在左树中执行直到找到包含o1和o2的子树的根节点，并返回该节点。

当到达最深层时会返回到上一层的递归调用处继续执行下一行代码。这是递归的特性。在这种情况下，当递归到达最底层叶子节点时，递归调用将返回到上一层递归调用处，继续执行下一行代码。

5.1.6例6：在二叉树中找到一个节点的后继节点

先在有一种新的二叉树节点类型如下

public class Node{public int value;public Node left;public Node right;public Node parent;public Node(int val){value=val;}
}

该结构比普通二叉树节点结构多了一个指向父节点的parent指针
假设有一棵Node类型的节点组成的二叉树，树中每个节点的parent指针都正确地指向自己的父节点，头节点的parent指向null。
只给一个在二叉树中的某个节点node，请实现返回node的后继节点的函数

在二叉树的中序遍历的序列中， node的下一个节点叫作node的后继节点。

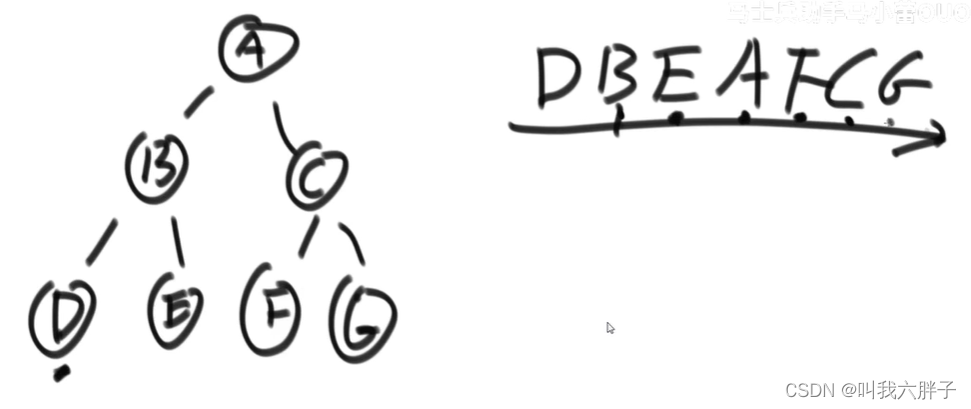
题意解析：正常来将需要中序排列才能找到后继节点，但是此时的时间复杂度为O(N)，当题中给出了指向父节点的指针，那么，如果两个节点之间真实距离为k的话能不能让时间复杂度变为O(k)

情况1：x有右树的时候，它的后继节点为他的右树上的最左节点

情况2：x无右树的时候，
看它的父节点，是不是它的父节点的左孩子，不是，
看它的父节点，是不是它的父节点的左孩子，不是，
看它的父节点，是不是它的父节点的左孩子，不是，
看它的父节点，是不是它的父节点的左孩子，是，
它的后继节点为此节点的父

因为对此节点来说，x是其左子树最右的节点

情况3：没有后继，当处于整个二叉树的最右侧最后一个节点是没有后继的

#include <iostream>struct Node {int val;Node* left;Node* right;Node* parent;Node (int val):val(val), left(nullptr), right(nullptr),parent(nullptr) {}
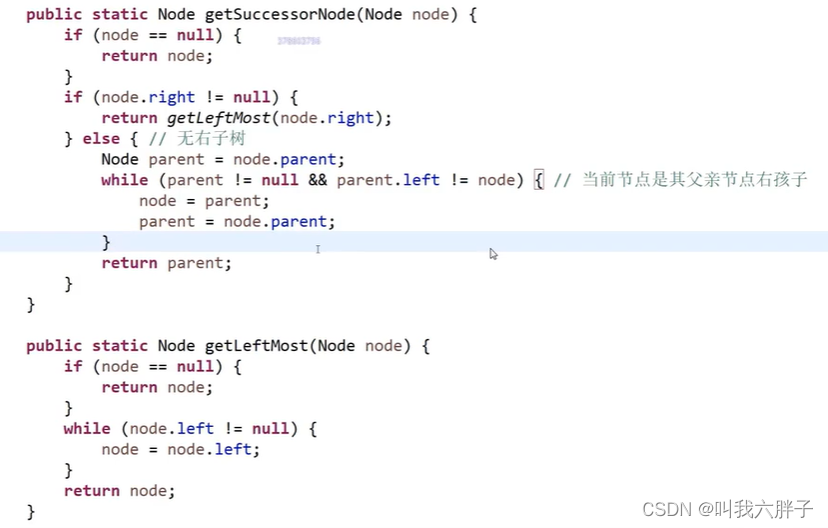
};Node* getMostLeftNode(Node* node) {if (node == nullptr) {return node;}while (node->left != nullptr) {node = node->left;}return node;
}Node* getNextNode(Node* node) {if (node == nullptr) {return node;}if (node->right != nullptr) {   // if node has right tree, we find the leftest nodereturn getMostLeftNode(node->right);} else {Node* parent = node->parent;while (parent != nullptr && parent->left != node) {node = parent;parent = node->parent;}return parent;}
}int main()
{Node* head = new Node(6);head->parent = nullptr;head->left = new Node(3);head->left->parent = head;head->left->left = new Node(1);head->left->left->parent = head->left;head->left->left->right = new Node(2);head->left->left->right->parent = head->left->left;head->left->right = new Node(4);head->left->right->parent = head->left;head->left->right->right = new Node(5);head->left->right->right->parent = head->left->right;head->right = new Node(9);head->right->parent = head;head->right->left = new Node(8);head->right->left->parent = head->right;head->right->left->left = new Node(7);head->right->left->left->parent = head->right->left;head->right->right = new Node(10);head->right->right->parent = head->right;Node* test1 = head->left->left;std::cout << test1->val <<  " next node: " <<  getNextNode(test1)->val << std::endl;Node* test2 = head->left->left->right;std::cout << test2->val <<  " next node: " <<  getNextNode(test2)->val << std::endl;Node* test3 = head->right->right;std::cout << test3->val <<  " next node: " <<  getNextNode(test3)<< std::endl;return 0;
}

5.1.7例7：二叉树的序列化和反序列化

就是内存里的一棵树如何变成字符串形式，又如何从字符串形式变成内存里的树
如何判断一颗二叉树是不是另一棵二叉树的子树?
由内存变为字符串叫序列化，由字符串还原为内存结构叫反序列化

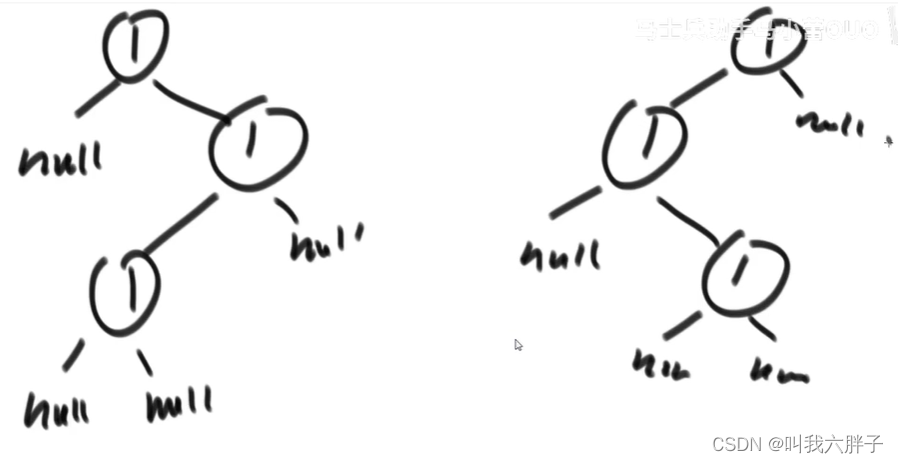
先序、中序、后序、按层等方式序列化都可以，以先序方式举例
例：
看图中左侧树
_ # _表示为空
来到头节点1：1
左孩子为空：1 _ # _
右孩子为1：1 _ # _ 1 _
右->左孩子为1：1 _ # _ 1 _ 1 _
右->左->左孩子为空：1 _ # _ 1 _ 1 _ # _
右->左->右孩子为空：1 _ # _ 1 _ 1 _ # _ # _
右->右孩子为空：1 _ # _ 1 _ 1 _ # _ # _ # _

看图中右侧树
来到头节点1：1
左孩子为1：1 _ 1 _
左->左孩子为空：1 _ 1 _ # _
左->右孩子为1：1 _ 1 _ # _ 1 _
左->右->左孩子为1：1 _ 1 _ # _ 1 _ # _
左->右->右孩子为1：1 _ 1 _ # _ 1 _ # _ # _
右孩子为空：1 _ 1 _ # _ 1 _ # _ # _ # _

以符号还原可以还原
1，#，1，1，#，#，#，
根据先序遍历
先1为头：#，1，1，#，#，#，
左孩子为空：1，1，#，#，#，
右孩子为1：1，#，#，#，
右->左孩子为1：#，#，#，
右->左->左孩子为空：#，#，
右->左->右孩子为空：#，
右->右孩子为空：

前序遍历序列化代码

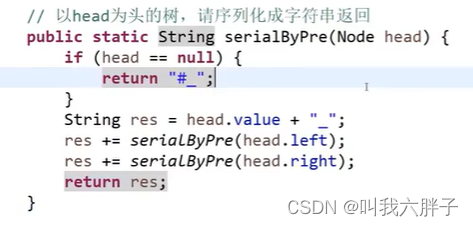
前序遍历反序列化代码

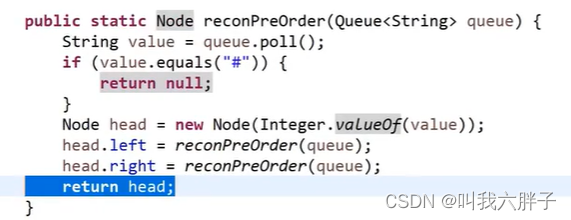
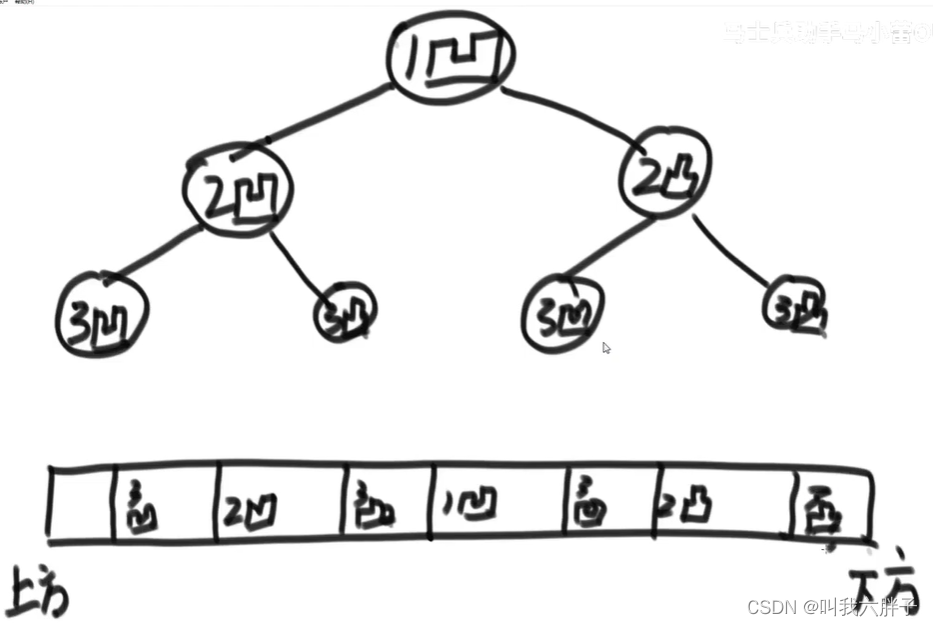
5.1.8例8：折纸问题

请把一段纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后展开。
此时折痕是凹下去的，即折痕突起的方向指向纸条的背面。
如果从纸条的下边向上方连续对折2次，压出折痕后展开，此时有三条折痕，从上到下依次是下折痕、下折痕和上折痕。
给定一个输入参数N，代表纸条都从下边向上方连续对折N次。请从上到下打印所有折痕的方向。
例如:N=1时，打印:down N=2时，打印:down down up

折纸发现，会在折痕上方出现凹折痕，在下方出现凸折痕


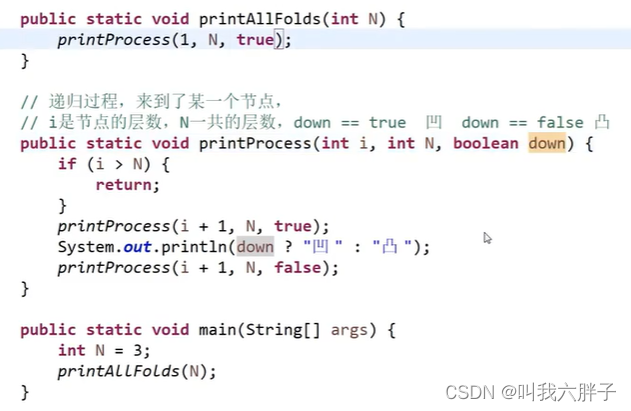
只用了N个空间