wordpress开发分类筛选上海高端seo公司

真值和机器数

真值：在日常的书写习惯中，往往用正、负号加绝对值表示数值，用这种形式表示的数值为真值。例如100D，-50D，-76O。

机器数：在计算机内部版使用的数，并且最高位表示符号的二进制数，又分为有符号数和无符号数。

无符号整数

无符号整数的定义

无符号整数：无符号整数即最高位不表示符号位，每一位都是数值位。

无符号整数的特征

无符号整数一般用来表示地址或者指针，因为地址不具有负的概念。

无符号整数的表示范围

n位的无符号整数可表示$0$~$2^n-1$的范围。

无符号整数的加法

无符号整数的加法，和普通的二进制加法没什么区别。

无符号数的减法

假设我们的mod是18，那么假设一个数是x，其在mod18下的补数就是18-x。
通过这种手段，我们可以将减法变成加法：前提是被减数>减数，即不溢出的情况下，可以得到正确的答案：例如9-3=[9+(18-3)]mod18=(9+15)mod18=(24)mod18=6。
而在无符号数的加法中，寄存器的位数实际上就已经充当了mod的作用，例如n位那么mod就是$2^n$。
通过将B全部位取反，末尾加1我们就可以得到B的补数。这个过程就和得到补码C对应-C的补码的过程一样。
其中通过这种方式得到补数的原理是这样的：因为A+A的补数=mod。
而B全部位取反+B就等于一个全1的序列，那么再将上1，自然就等于mod了。
所以取反+1就为补数。

有符号整数(定点整数)

有符号整数的定义

定点整数：定点整数是纯整数，简单来说就是不含小数，小数点在数值位之后。
若数据X的表示形式为X=$x_0,x_1{x}_2...x_n$其中$x_0$是符号位，剩下的数值位$x_1$~$x_n$是尾数，$x_n$为最低有效位。
有符号整数分为：原码，反码，补码，移码。

原码

原码：最高位表示符号位，具有位权，可表示整数和小数。

原码的特点

优点：和真值的对应关系简单，直观，与真值的转换简单，用原码实现乘除运算比较简便，无论是正数原码还是负数原码，比较大小很容易判断。

缺点：
1.0的表示不唯一，有两种方式表示真值0，分别是(+0)00000000和(-0)10000000
2.加减法运算比较复杂，这很好理解，如果不复杂当前计算机就不会使用补码运算了。
3.符号位不可以参与运算

反码

反码：最高位表示符号位，正数反码具有位权，负数反码无位权,可表示整数和小数。

反码的特点

缺点：
1.0的表示不唯一，00000000(+0)和11111111(-0)
2.表示范围比补码小，在计算机中很少使用，一般用作数码变换的中间形式(其实也就是原反补变换的中间形式)
4.符号位不可以参与运算

补码

最高位表示符号位，正数补码具有位权，负数补码无位权。可表示整数和小数。

补码的特点

优点：
0的表示唯一，即+0(00000000)
符号位和数值位可以参与运算

缺点：
负数补码不容易判断大小。

快速求解n位负数补码的方法

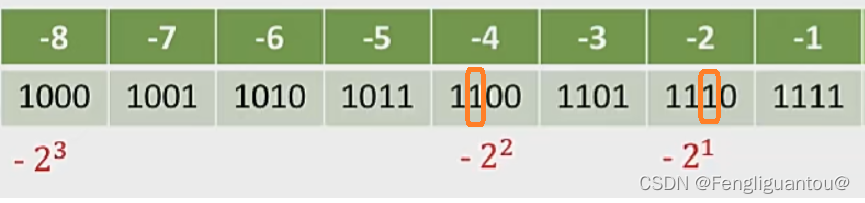
这里的最高位就是符号位，因为负数补码的符号位固定为1，所以假设总共有4位。可以看出真值$-2^n$的补码就是按照权重找到对应位，然后将这一位和这一位左边全置1就能得到。
并且还能看出一个特征，即负数补码的数值位越大，真值越大。

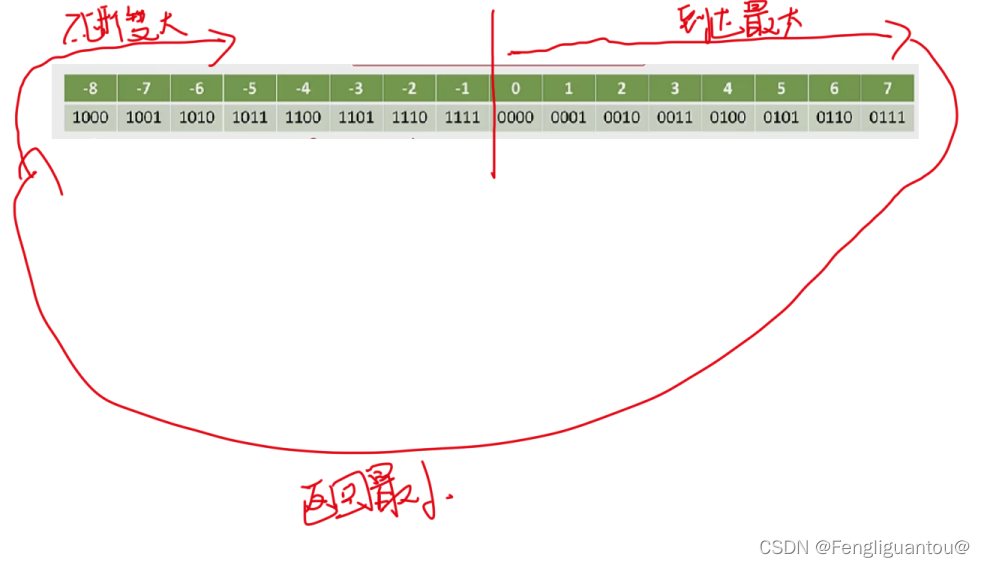
对于补码小数，上面的结论还能成立？

为什么补码能够多表示一个范围(重点)

首先，前提是机器字长为8位，原码和反码在表示过程中是一一对应的，但是两者都具有一个冗余状态，原码的1000000和反码的11111111，这两个冗余状态通过原反补转换成补码时，因为溢出原因会变成0000 0000，这就导致补码中的0只有一种表示方式，这就导致补码的1000 0000这个状态没有数字可以表示，但是通过原反补的规则，因为溢出问题的存储，原码和反码的任何一个状态都不可能转换为1000 0000，所以计算机规定原码为1000 0000和反码的1111 1111转换为补码时，直接映射成1000 0000，补码的1000 0000不需要经过原反补转换，解释的时候直接解释为1000 0000。

变形补码

移码

移码：不具有位权，常用来表示浮点数的阶码，只能表示整数。

移码的特点

优点：
1.只有一种方式表示0，即(+0)1000 0000。
2.符号位为1表示真值为正，符号位为0表示真值为负。
3.从下面这个图可以看出，移码的递增有点类似无符号整数，所以移码很方便硬件电路对比大小。

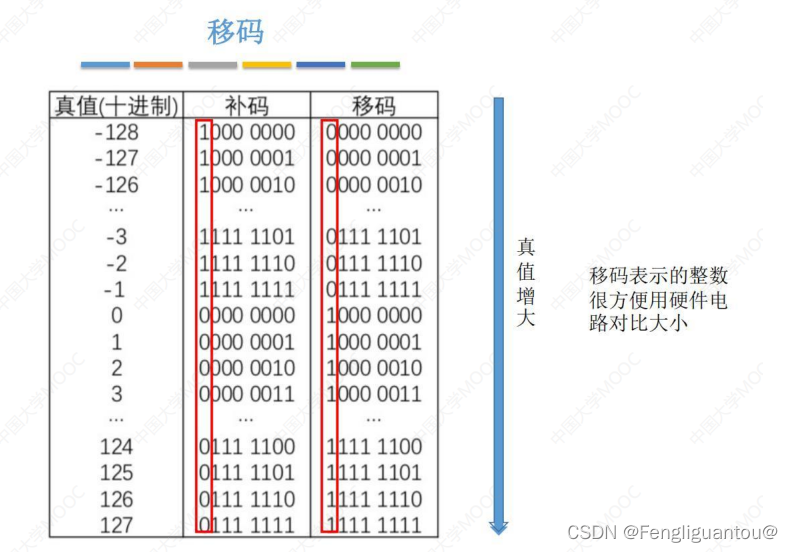
x的移码和-x的移码转变似乎也是全部位按位取反，末尾加1，这个不知道准不准确。

有符号数，无符号整数的范围表示

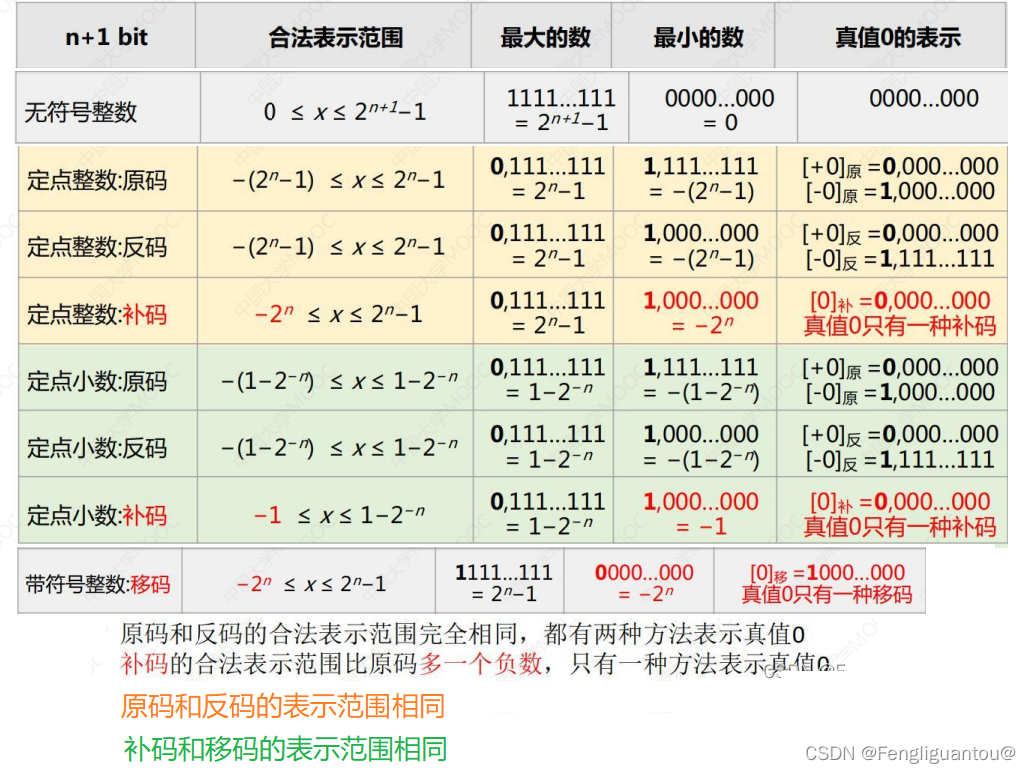
注意：定点小数虽然说能够表示这么大的范围，但是不是范围里的每个数字都能够使用定点小数准确表示出来，因为其不是和定点整数一样从0开始每次递增的。

定点整数中，补码比原码和反码多表示一个$-2^n$，注意是只多表示这一个数字，因为二进制整数每次的差距至少为1
定点小数中，补码比原码和反码同样也只是多表示了-1这一个数字。
一定要注意，这里是只，不论是定点整数还是小数，补码都只是比原码多表示了一个数字。

判断两个数的和是否溢出

题目一：机器字长8位，两个数字用原码表示，A是原码表示的-64，B是原码表示的-64，两者的结果同样用原码表示，是否会溢出？

答案是会的，因为原码只能表示-127-127

题目二：机器字长8位，两个数字用补码表示，A是补码表示的-64，B是补码表示的-64，两者的结果同样用补码表示，是否会溢出？

答案是不会，因为补码可以表示-128，127

无符号数和有符号数如何进行减法运算

无论是无符号整数，还有补码， 在求-x的时候，都是如下的操作。

方法：将减数进行求补，然后将负号改为正号，被减数和求补以后的减数相加。

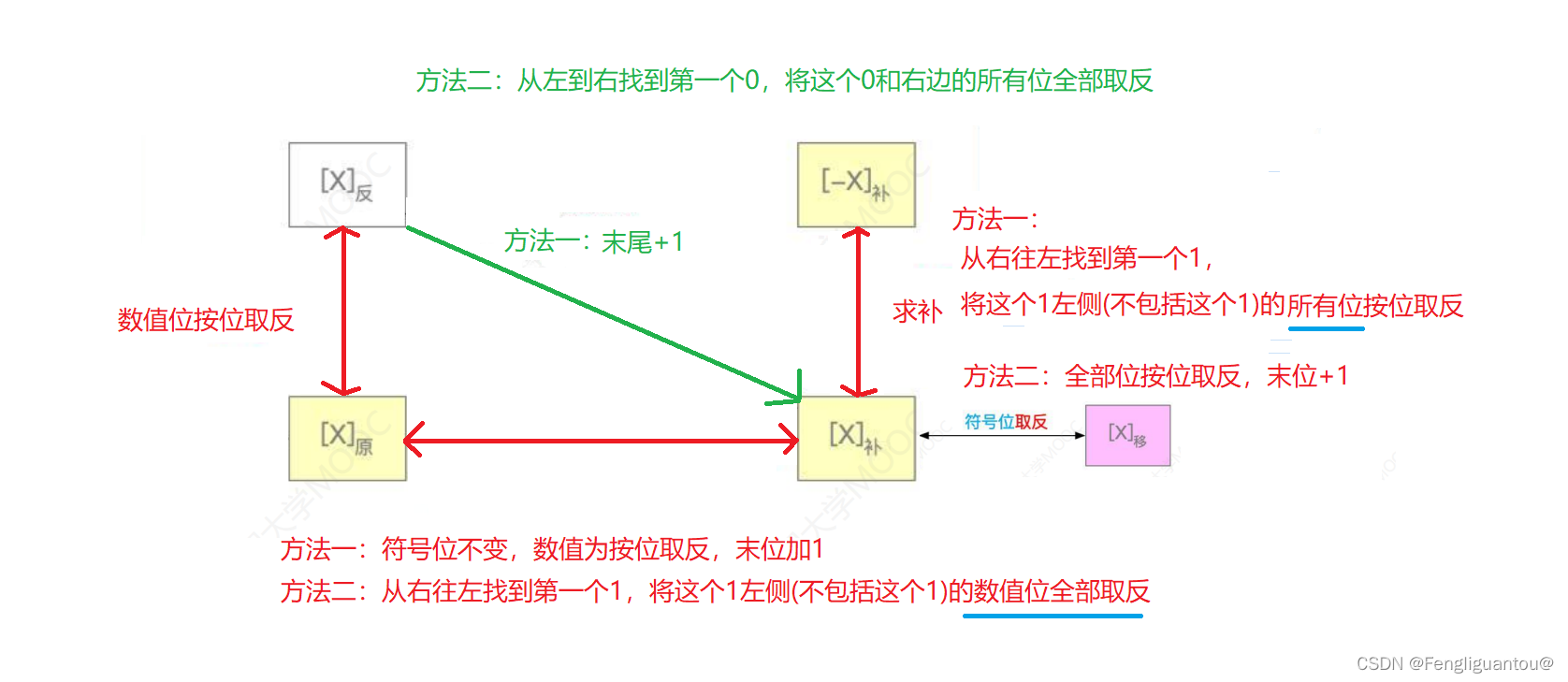
求补有两种方法：

方法一：全部位按位取反，末尾+1

方法二：从右往左找到第一个1，将这个1左侧的所有位(不包括这个1)全部取反。

为什么要使用加法电路来完成减法？

加法电路造价便宜，判断比较容易。

事实上，无符号的减法我们不是一定要通过上述方式完成，因为无符号是不具有符号位的，上述方式是计算机内部无符号的计算方式，如果是我们手算，我们可以直接两个数相减即可。不用进行什么取补然后减法变加法的操作。

原码，反码，移码，补码的互相转换

定点小数

定点小数：定点小数是纯小数，简单来说就是不含整数，小数点在符号位之后，数值位之前。若数据X的表示形式为X=$x_0,x_1{x}_2...x_n$其中$x_0$是符号位，剩下的数值位$x_1$~$x_n$是尾数，$x_1$为最高有效位。

定点整数和定点小数的原码定义

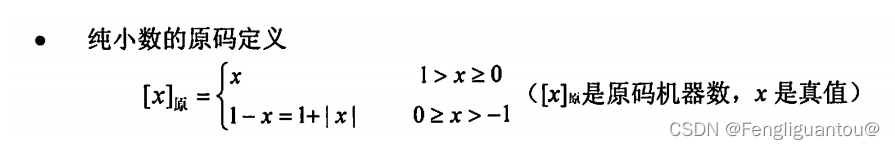
纯小数(假设机器字长为n+1位)：
当$x\ge 0$ 时，当$x\ge 0$ 时，$x$的原码可由真值$x$通过二进制转换得到。
当$x\le 0$ 时，$x$的原码需要由$1+|x|$以后的真值通过二进制转换得来。
当真值等于0的时候，因为定点小数的原码具有两种形式，所以同样可以使用上述两种方式，分别是0000000和10000000

例如：
当机器字长为8位时，当x=0.5时，其原码由0.5转换而来，结果为0.1000000
当x=-0.5时，其原码由1-(-0.5)=1+0.5=1.5转换而来，结果为1.1000000

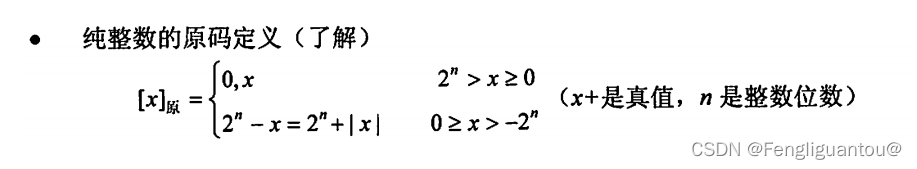
纯整数(假设机器字长为n+1位)：
当$x\ge 0$ 时，$x$的原码可由真值$x$通过二进制转换得到。
当$x\le 0$ 时，$x$的原码需要由$2^n+|x|$以后的真值通过二进制转换得来。
真值为正时，很好理解，可以直接通过二进制转换得到原码。
真值为负时，因为符号的原因，所以需要对真值取绝对值并且加上$2^n$，其本质就是加上二进制最高位的符号位。
当真值等于0时，因为定点原码的真值具有两种表现形式，00000000和1000000所以真值0变成原码的时候也可以使用上述两种方式。
例如：
当机器字长为8时，当x=5时，5的原码由真值5转换得来，结果为为0.0000101
当x=-5时，-5的原码由 $2^8-(-5)=2^8+5$真值转换而来，结果为
1.0000101

总结：
真值为正时，原码可以由真值直接转换得来。

真值为负时，需要对真值取绝对值并加上对应机器字长二进制对应的符号位，小数就直接加上1即可，整数就加上二进制最高位对应的真值。然后用真值转换成原码。
本质都是通过真值加上某个数，从而修改对应二进制的符号位，将符号位的0变成1。

这里的定义，其实本质上就是如果通过真值，不考虑符号位的情况下，直接转换二进制得到对应的原码。因为实际上真值为负时，我们可以通过符号位取1的方式，然后按照原反补的方式得到原码，而这种定义方式就是不靠这种方法，因为最终通过定义，真值变成了正数，这时候就不需要考虑符号位了，并且因为正数的原反补相同。

定点小数和定点整数的补码定义

假设机器字长为n+1位。
定点整数的补码定义：
当真值为正时，补码直接由真值通过二进制转换得到
当真值为负时，补码需要由 $2^{n+1}-|真值|$的结果通过二进制转换得到。
实际上就是mod-真值的绝对值。当有n位时，mod就是$2^n$

这里的定义，其实本质上就是如果通过真值，不考虑符号位的情况下，直接转换二进制得到对应的补码。因为实际上真值为负时，我们可以通过符号位取1的方式，然后按照原反补的方式得到补码，而这种定义方式就是不靠这种方法。因为最终通过定义，真值变成了正数，这时候就不需要考虑符号位了，并且因为正数的原反补相同。

移码的定义(目前还不懂)

移码本质就是加了一个偏执常量，当机器字长为n+1时，真值为x的移码，需要由x+$2^n$转换得到。这时偏执常量就是$2^n$

可表示的不同数字的个数 和 可表示范围

可表示的数字个数：是站在状态上来进行思考的，一个二进制可以表示2种状态，n个二进制位就可以表示$2^n$个状态，当然原码和反码会少1个。
可表示的范围：是站在位权来进行考虑的，因为二进制的位权是从0开始，只有正/负原码，正数反码和补码可以这样计算使用位权来计算范围。但是负数的补码和反码不能这样计算范围，因为其没有位权这个。

原码，反码，补码表示的定点小数个数

假设机器字长为n+1，站在状态的角度上，可以表示$2^n+2^n$个状态，但是由于0有两种表示，所以有状态重叠，所以只能表示$2^n+2^n=2^{n+1}-1个不同数字$，反码也是如此。
补码因为没有状态重叠，所以可以表示$2^{n+1}$个不同的状态。

负数反码和补码比较大小的方式(重要)

负数反码和原码比较只需要遵循一个原则：数值位越大，真值越大。

一个数什么时候可能会溢出

一个数只有在全1的时候再加1或者大于1的数才会溢出。

关于原反补运算的特点

实际上正数原码和反码，补码的符号位都可以参与运算，因为补码的符号位可以参与运算，所以正数原码和反码也可以，但是负数的原码和反码无法做到符号位参与运算，所以计算机中的加减法在不对符号位处理的前提下只能由补码完成。

十六进制数的取反

十六进制数数位的取反=15-该数位的数字
例如F1取反以后变成0E。