外包加工平台小红书seo软件

105. 从前序与中序遍历序列构造二叉树

文章目录

• • • [105. 从前序与中序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)
    • • 一、题目
      • 二、题解

---

一、题目

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

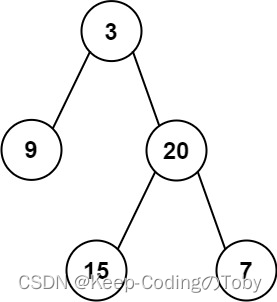
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

二、题解

算法思路：

我们要根据给定的前序遍历和中序遍历序列构建出一棵二叉树。前序遍历序列告诉我们根节点的值以及左子树和右子树的分割点，中序遍历序列告诉我们左子树和右子树的节点排列顺序。我们可以通过递归的方法来实现构建二叉树的过程。

具体步骤如下：

1. 从前序遍历序列中取出第一个元素，它是当前子树的根节点的值。
2. 在中序遍历序列中找到该根节点的值，根据这个值，将中序序列划分为左子树部分和右子树部分。
3. 根据左子树和右子树的节点数量，在前序遍历序列中划分出左子树的前序序列和右子树的前序序列。
4. 递归地构建左子树和右子树。

具体实现：

class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {// 基准情况：如果前序遍历序列为空，返回空指针表示空树if (preorder.size() == 0) {return nullptr;}// 创建当前子树的根节点TreeNode *root = new TreeNode();root->val = preorder[0];// 在中序遍历序列中找到根节点的位置int index = 0;for (index = 0; index < inorder.size(); index++) {if (inorder[index] == preorder[0]) {break;}}// 划分左子树和右子树的序列vector<int> leftPreorder(preorder.begin() + 1, preorder.begin() + index + 1);vector<int> leftInorder(inorder.begin(), inorder.begin() + index);vector<int> rightPreorder(preorder.begin() + index + 1, preorder.end());vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());// 递归构建左子树和右子树root->left = buildTree(leftPreorder, leftInorder);root->right = buildTree(rightPreorder, rightInorder);return root;}
};

算法分析：

• 时间复杂度：在每次递归中，我们都需要遍历中序遍历序列来找到根节点的位置，这需要 O(n) 的时间，其中 n 是节点数量。递归的总时间复杂度取决于递归的层数以及每层的操作，因此总体时间复杂度为 O(n)。

• 空间复杂度：每次递归都会创建新的前序和中序序列，空间复杂度主要取决于递归的深度，最坏情况下递归深度为 n，所以空间复杂度为 O(n)。此外，还需要存储二叉树节点的空间，所以总体空间复杂度也为 O(n)。