---

如何使用递归构建二叉树

1、创建一颗全新树（题1-5）

构造树一般采用前序遍历，因为先构造中间节点，然后递归构造左子树和右子树。

TreeNode* newtree = new TreeNode(val);   // 每次递归都new一个节点
if(..) return newtree;      // 直接返回这个root
newtree->left = 递归函数(....)    // 用这个新建节点的左去接递归函数的返回值
newtree->right = 递归函数(....) 
return newtree;

2、在原有的树上新增东西（题6）

删除二叉树节点，增加二叉树节点，用递归函数的返回值来完成。

输入为root
if (root == nullptr) {TreeNode* temp = new TreeNode(val);   // 在树上新加的节点return temp;
}root->left = insertIntoBST(root->left, val);
root->right = insertIntoBST(root->right, val);return root;  // return输入的root

1 106 从 后序 与 中序 遍历序列构造二叉树

1和2为同一类型，题外话：
前序和中序可以唯一确定一棵二叉树。
后序和中序可以唯一确定一棵二叉树。

但前序和后序不能唯一确定一棵二叉树！因为没有中序遍历无法确定左右部分，也就是无法分割。

设有一颗二叉树：

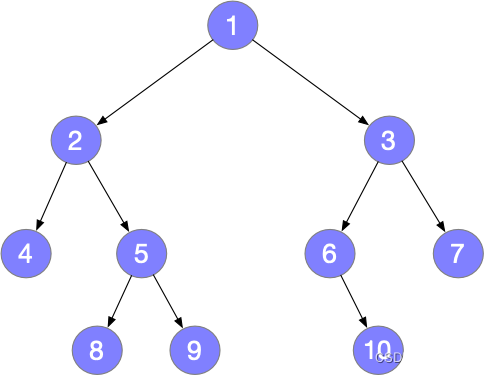
树的遍历结果可得两个规律：
1、在后序遍历序列中,最后一个元素为树的根节点
2、在中序遍历序列中,根节点的左边为左子树，根节点的右边为右子树

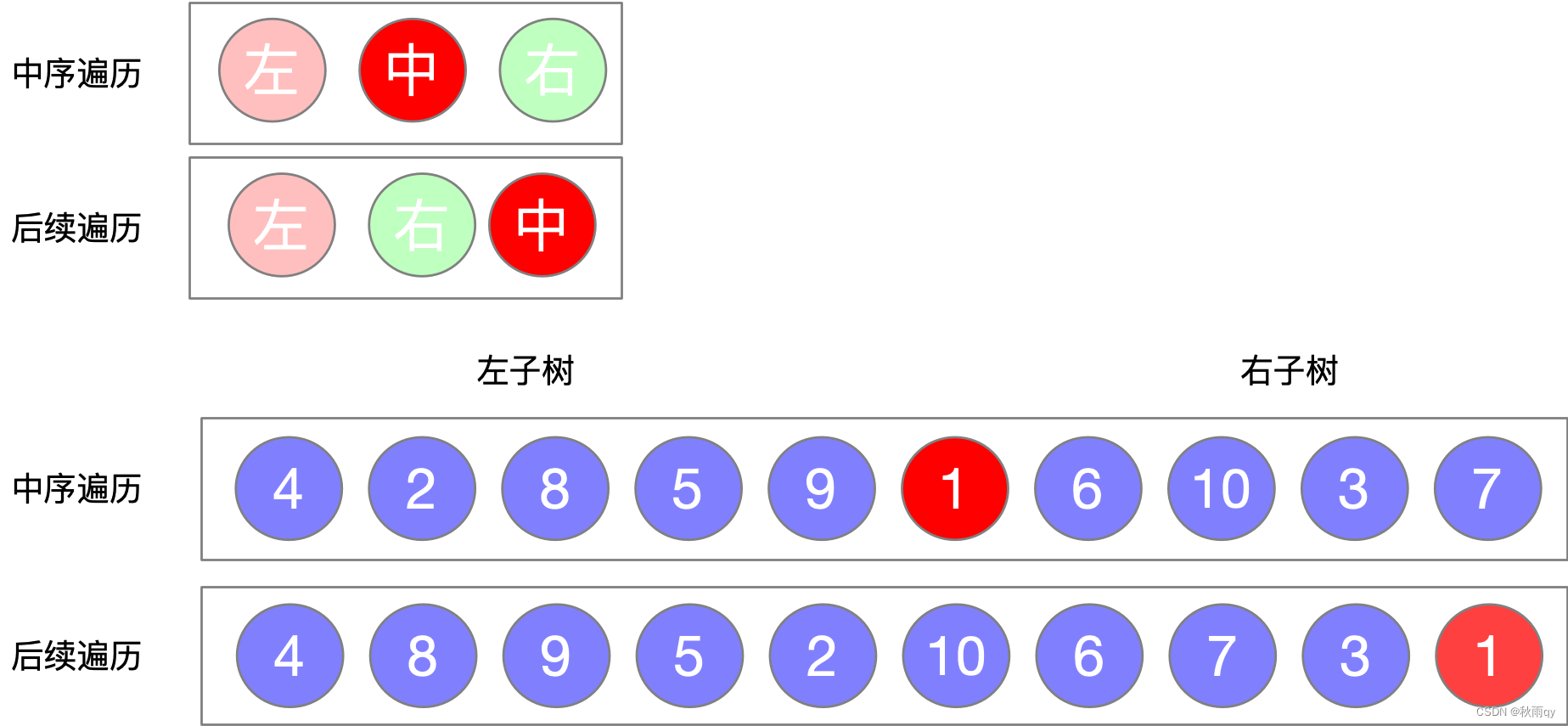
根据特性还原，步骤如下

1、输入中序和后序（如果是空数组就退）
2、处理后序：找到根节点(后序最后一个元素)（如果后序只有一个元素了直接返回）
3、处理中序：中序中根节点的位置
4、将中序分为左、右子树
5、得到后序的左、右子树
6、子树作为下一次递归的输入

步骤拆解伪代码如下：

// 第一步
if (postorder.size() == 0) return NULL;// 第二步：后序遍历数组最后一个元素，就是当前的中间节点
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
// 叶子节点
if (postorder.size() == 1) return root;// 第三步：确认根节点在中序中的位置
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;
}// 第四步：切割中序数组，得到 中序左数组和中序右数组
// 第五步：切割后序数组，得到 后序左数组和后序右数组// 第六步
root->left = traversal(中序左数组, 后序左数组);
root->right = traversal(中序右数组, 后序右数组);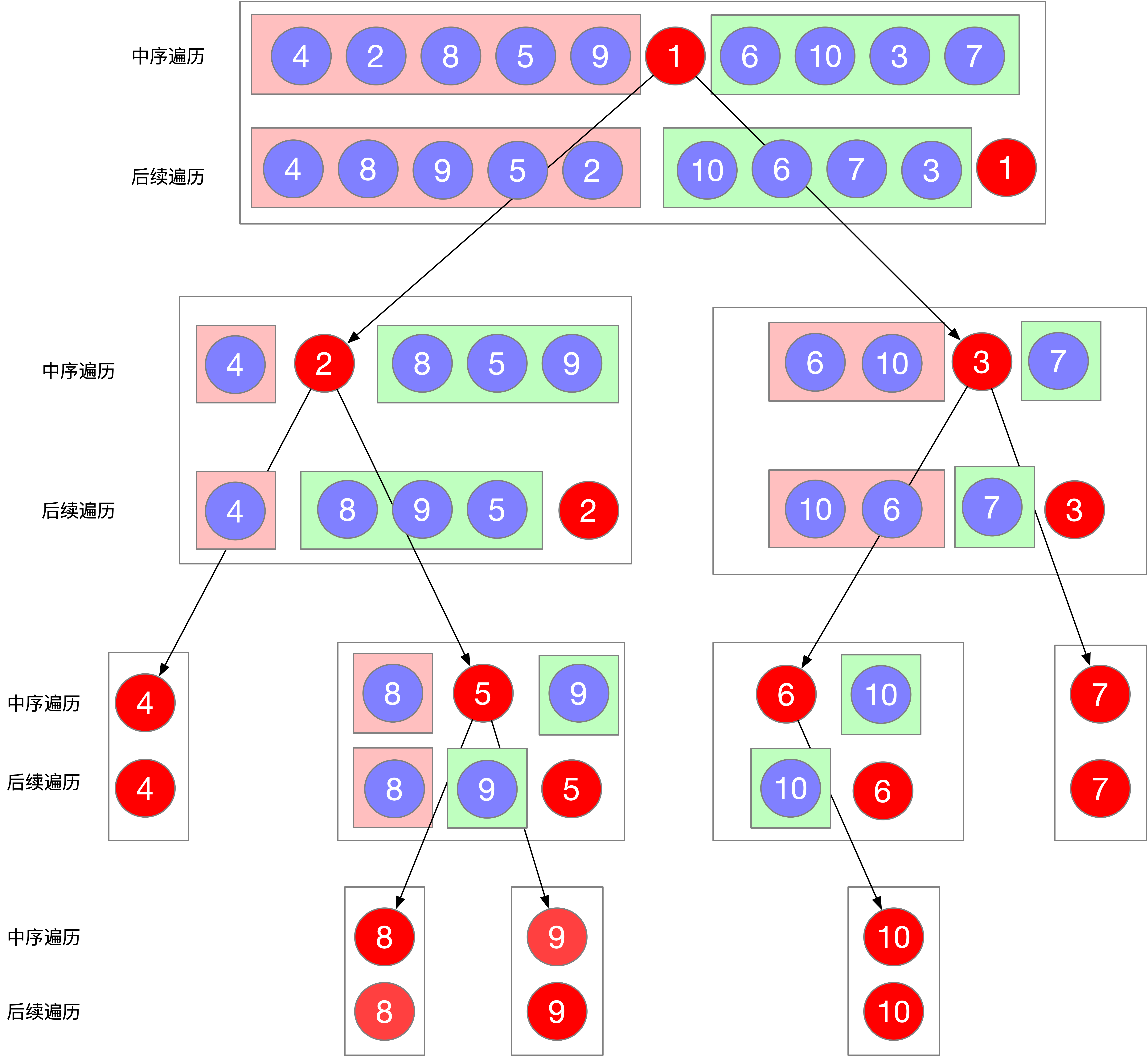

第4和第5尤其重要，如何将输入的中序和后序分割为中序左右树和后序左右树尤为关键

4、将中序分割左右子树

// 找到根节点在中序中的位置(中序的切割点)
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;
}// 左闭右开区间：[0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end)  注意这里加1，因为要跳过根节点，下面分割后序不加。
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end());

5、后序数组的切割点怎么找？
后序的根节点在最后，不像中序可以靠根节点来分割左右子树。
此时有一个必然条件，中序数组大小一定是和后序数组的大小相同的，后序数组就可以按照左中序数组的大小来切割，切成左后序数组和右后序数组。

// postorder 舍弃末尾元素，因为这个元素就是中间节点，已经用过了
postorder.resize(postorder.size() - 1);// 左闭右开，注意这里使用了左中序数组大小作为切割点：[0, leftInorder.size)
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
// [leftInorder.size(), end)   注意这里不加1，前面分割中序时加
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

整体代码如下

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int sizeinorder = inorder.size();int sizepostorder = postorder.size();if (sizepostorder == 0) return nullptr;int rootValue = postorder[sizepostorder - 1];  // 根节点的值TreeNode* newtree = new TreeNode(rootValue);if (sizepostorder == 1) return newtree;int delimiterIndex;for (delimiterIndex = 0; delimiterIndex < sizeinorder; delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}vector<int> inorderleft(inorder.begin(), inorder.begin() + delimiterIndex);vector<int> inorderright(inorder.begin() + delimiterIndex + 1, inorder.end());vector<int> postorderleft(postorder.begin(), postorder.begin() + inorderleft.size());vector<int> postorderright(postorder.begin() + inorderleft.size(), postorder.end() - 1);newtree->left = buildTree(inorderleft, postorderleft);newtree->right = buildTree(inorderright, postorderright);return newtree;
}

2 105 从 前序 与 中序 遍历序列构造二叉树

注意看分割时的索引

TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int sizepreorder = preorder.size();int sizeinorder = inorder.size();if (sizepreorder == 0) return nullptr;int rootval = preorder[0];TreeNode* newtree = new TreeNode(rootval);if (sizepreorder == 1) return root;int inrootindex;for (inrootindex = 0; inrootindex < sizeinorder; ++inrootindex) {if (inorder[inrootindex] == rootval) break;}vector<int> inorderleft(inorder.begin(), inorder.begin() + inrootindex);vector<int> inorderright(inorder.begin() + inrootindex + 1, inorder.end());vector<int> preorderleft(preorder.begin() + 1, preorder.begin() + 1 + inorderleft.size());vector<int> preorderright(preorder.begin() + 1 + inorderleft.size(), preorder.end());newtree->left = buildTree(preorderleft, inorderleft);newtree->right = buildTree(preorderright, inorderright);return newtree;
}

3 108 将有序数组转换为二叉搜索树（输入）

二分法复习，数组的mid就是根节点
1、输入输出
TreeNode* construct(vector<int>& nums, int left, int right)
输入一个数组nums，返回一个从nums[left]到nums[right]的元素构建一棵树
2、左指针大于右指针退出递归
if (left > right) return nullptr;
3、使用二分法找到这一区间[left, right]中的中间值mid，记为nums[mid]，从而确定根节点的值。(本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间)

问题：数组长度为偶数，中间节点有两个，取哪一个？实际上取哪一个都可以，答案都对。
int mid = (left + right) / 2;，这么写其实有一个问题，就是数值越界，例如left和right都是最大int，这么操作就越界了，在二分法中尤其需要注意！求mid写做：int mid = left + ((right - left) / 2);

int mid = left + ((right - left) / 2);
TreeNode* newtree = new TreeNode(nums[mid]);
newtree->left = traversal(nums, left, mid - 1);
newtree->right = traversal(nums, mid + 1, right);
return newtree;

4、整合

class Solution {
private:TreeNode* traversal(vector<int>& nums, int left, int right) {if (left > right) return nullptr;int mid = left + ((right - left) / 2);TreeNode* root = new TreeNode(nums[mid]);root->left = traversal(nums, left, mid - 1);root->right = traversal(nums, mid + 1, right);return root;}public:TreeNode* sortedArrayToBST(vector<int>& nums) {TreeNode* root = traversal(nums, 0, nums.size() - 1);return root;}
};

4 654 最大二叉树（输入很难想）

递归

构造树一般采用前序遍历，因为先构造中间节点，然后递归构造左子树和右子树。

1、输入输出
TreeNode* construct(vector<int>& nums, int left, int right)
输入一个数组nums，返回一个从nums[left]到nums[right]的元素构建一棵树
2、左指针大于右指针退出递归
if (left > right) return nullptr;
3、找到这一区间[left, right]中的最大值的索引maxindex，记为nums[maxindex]，这样确定根节点的值，随后进行递归。

int maxindex = left;
for (int i = left + 1; i <= right; ++i) {if (nums[i] > nums[maxindex]) {maxindex = i;}
}
// 找最大值索引TreeNode* node = new TreeNode(nums[maxindex]);
node->left = construct(nums, left, maxindex - 1);
node->right = construct(nums, maxindex + 1, right);
return node;

4、整合

class Solution {
public:TreeNode* bfs(vector<int>& nums, int left, int right){if(left > right){return nullptr;}int maxindex = left;for(int i = left + 1; i <= right; ++i){if(nums[i] > nums[maxindex]) maxindex = i;}TreeNode* newtree = new TreeNode(nums[maxindex]);newtree->left = bfs(nums, left, maxindex-1);newtree->right = bfs(nums, maxindex+1, right);return newtree;}TreeNode* constructMaximumBinaryTree(vector<int>& nums) {return bfs(nums, 0, nums.size()-1);}
};

单调栈

之后补充

5 617 合并二叉树

TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if (root1 == nullptr && root2 == nullptr) return nullptr;if (root1 == nullptr) return root2;if (root2 == nullptr) return root1;TreeNode* newtree = new TreeNode(root1->val + root2->val);newtree->left = mergeTrees(root1->left, root2->left);newtree->right = mergeTrees(root1->right, root2->right);return newtree;
}

6 701 二叉搜索树中的插入操作（重点独立重做）

在原有的树上新增东西

TreeNode* insertIntoBST(TreeNode* root, int val) {if (root == nullptr) {TreeNode* temp = new TreeNode(val);return temp;}// TreeNode* temp = new TreeNode(root->val);if (root->val > val) {root->left = insertIntoBST(root->left, val);}if (root->val < val) {root->right = insertIntoBST(root->right, val);}// return temp;return root;
}

7 450 删除二叉搜索树中的节点（中等题）

8 538 把二叉搜索树转换为累加树