东莞做网站 信科网络网上推广赚钱项目

前言

Aho Corasick Algorithm又叫AC自动机，该算法是一个匹配算法，用来匹配文本Text中多个patterns分别出现的次数；

我们定义n为patterns的总长度；m为Text的长度；

问题：在ahishershe文本中找出以下"he", "she", "hers", "his"各个patterns出现的次数；

最直接的暴力解法时间时间复杂度为O(n*m)，如果采用KMP Algorithm，会把时间度降低为O(n+m)，但是这是在单一的pattern的情况下，在k个pattern的情况下，应该成倍的增长m，时间复杂度为O(n+k*m)，使用Aho Corasick Algorithm可以把时间优化为O(n+m+z)，其中z表示出现的次数；

介绍

AC自动机利用的前缀树Trie这一数据结构；前缀树是一种很简单的结构，其构造如下：

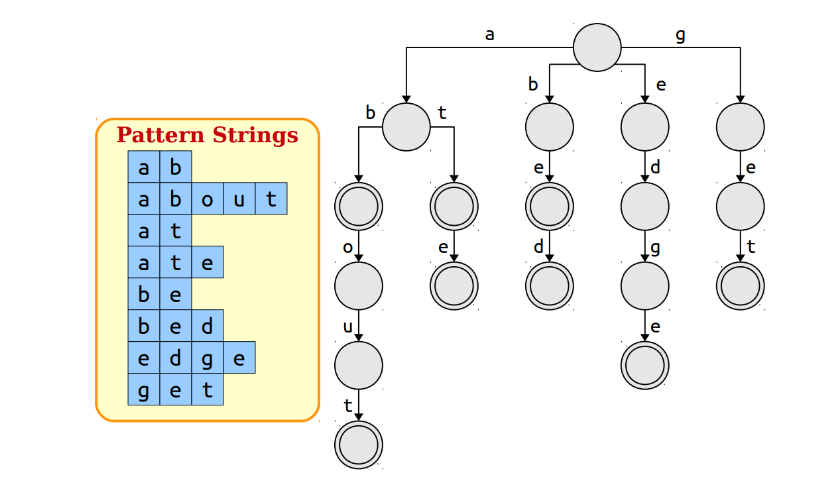
我们可以构建Trie然后使用窗口进行暴力搜索，其时间复杂度为O(m*max(L))，这里面的max(L)是Trie的深度；

这里面可以优化的一个点是，我们可以利用不匹配词的最长后缀作为词的前缀去优化查找，而不是不匹配就重新从root开始；找到最长的公共后缀将保证我们不需要再次检查那么多字符串，并且在每次不匹配之后我们都会重复上一步骤；

如图所示：

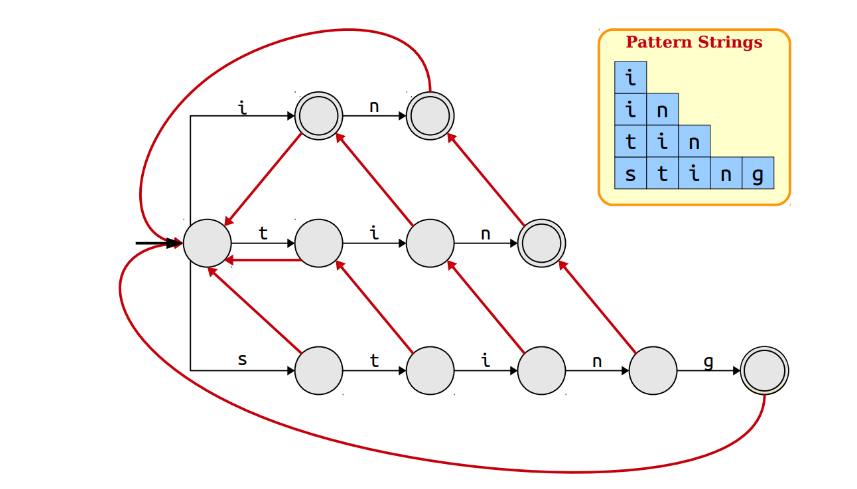
这些指向最长后缀的节点的链接被称为suffix links或failure links，在匹配不成功的时候，若有最长的后缀节点，指向最长的后最节点，若没有则指向root进行重新查找；

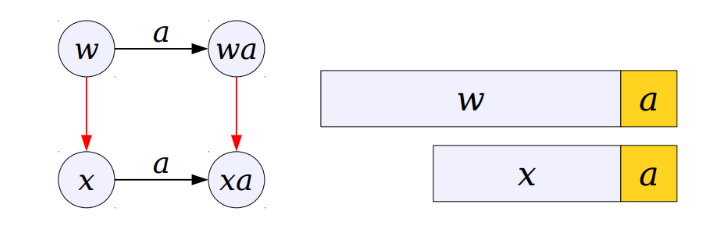
假设在一颗Trie上有字符串w,x,...，其中x是w的最长的后缀，所以有红线连接w和a，若存在wa和xa，这xa也是wa的最长后缀，也用红线连接；

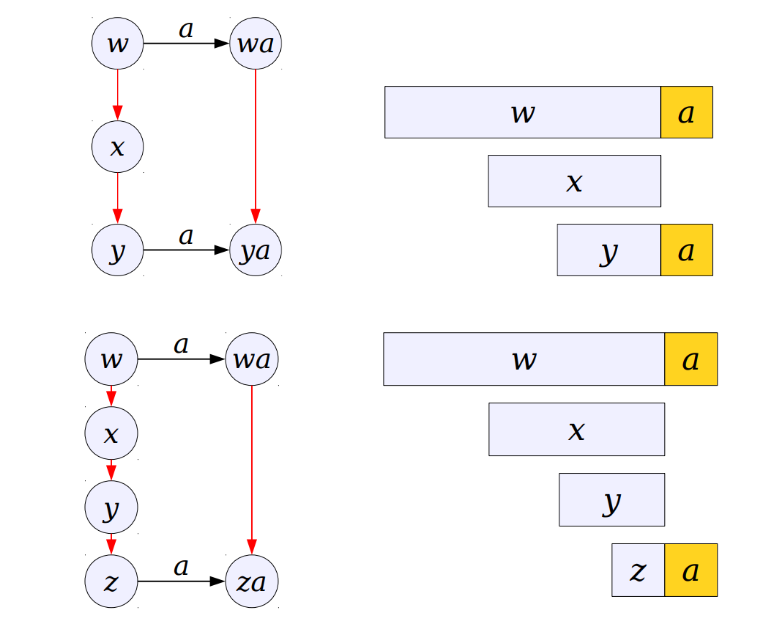
若xa不存在，就去找除了x以外的和w的最大公共后缀，如果发现y符合条件，可以对y进行匹配；如果y不符合条件，就接着找除了x,y以外的和w的最大公共后缀，依次进行；

其次需要优化的一点输出环节，如果pattern1是pattern2的后缀的情况下，我们可能会忽略掉pattern1，所以在寻找最大后缀时需要进行判断，如果最大后缀结点是pattern，就用output link连接原结点指向该结点，在以该结点为原结点去连接，直到root；如果不是就判断该结点的最大后缀结点是否是pattern，再用原结点去连接这一个结点；

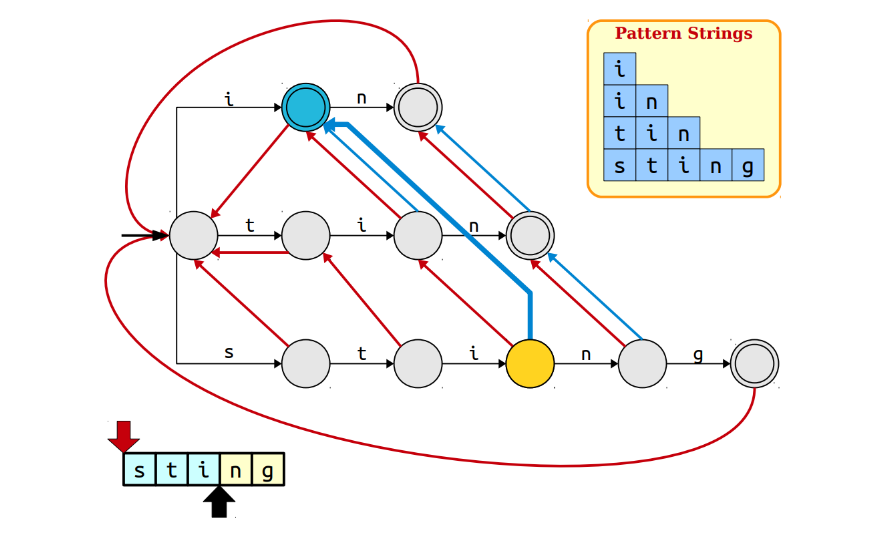
在文本sting中，遍历到i的时候，可以发现sti的最大后缀ti并不是pattern，于是就找ti的最大后缀i，是pattern，于是用蓝色的线把sti和i结合起来；这里加粗了这一过程；

在遍历到n的时候，发现tin和in都是pattern，依次进行连接

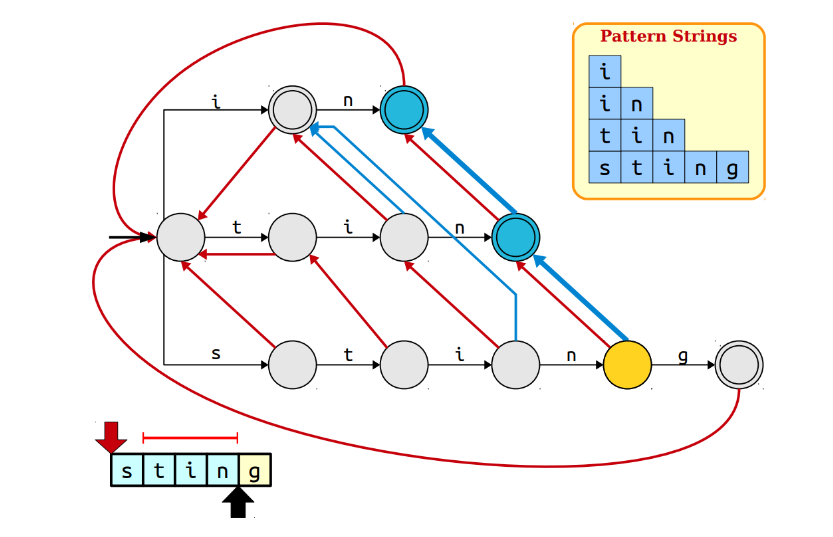
这时时间复杂度为O(m+z)，其中z表示pattern的出现次数；

实现

下面是python实现的代码：

from collections import defaultdictclass ahocorasick:def __init__(self, words):self.max_states = sum([len(word) for word in words])self.max_characters = 26self.out = [0] * (self.max_states + 1)self.fail = [-1] * (self.max_states + 1)self.goto = [[-1] * self.max_characters for _ in range(self.max_states + 1)]for i in range(len(words)):words[i] = words[i].lower()self.words = wordsself.states_count = self.__build_matching_machine()def __build_matching_machine(self):k = len(self.words)states = 1for i in range(k):word = self.words[i]current_state = 0for character in word:ch = ord(character) - 97if self.goto[current_state][ch] == -1:self.goto[current_state][ch] = statesstates += 1current_state = self.goto[current_state][ch]self.out[current_state] |= (1 << i)for ch in range(self.max_characters):if self.goto[0][ch] == -1:self.goto[0][ch] = 0queue = []for ch in range(self.max_characters):if self.goto[0][ch] != 0:self.fail[self.goto[0][ch]] = 0queue.append(self.goto[0][ch])while queue:state = queue.pop(0)for ch in range(self.max_characters):if self.goto[state][ch] != -1:failure = self.fail[state]while self.goto[failure][ch] == -1:failure = self.fail[failure]failure = self.goto[failure][ch]self.fail[self.goto[state][ch]] = failureself.out[self.goto[state][ch]] |= self.out[failure]queue.append(self.goto[state][ch])return statesdef __find_next_state(self, current_state, next_input):answer = current_statech = ord(next_input) - 97while self.goto[answer][ch] == -1:answer = self.fail[answer]return self.goto[answer][ch]def search_words(self, text):text = text.lower()current_state = 0result = defaultdict(list)for i in range(len(text)):current_state = self.__find_next_state(current_state, text[i])if self.out[current_state] == 0: continuefor j in range(len(self.words)):if (self.out[current_state] & (1 << j)) > 0:word = self.words[j]result[word].append(i - len(word) + 1)return resultif __name__ == "__main__":words = ["he", "she", "hers", "his"]text = "ahishershe"aho_chorasick = ahocorasick(words)result = aho_chorasick.search_words(text)for word in result:for i in result[word]:print("Word", word, "appears from", i, "to", i + len(word) - 1)

参考

Aho Corasick Algorithm (opengenus.org)